Сложение матриц. Действия над ними

Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов данных двух матриц . Символически это записывают .

Пример 1.

Аналогично определяетсяразность двух матриц.

Сложение матриц обладает переместительным и сочетательным свойствами, т.е. 1.) ;

2.) .

Умножение матрицы на число

Чтобы умножить матрицу на число , нужно каждый элемент этой матрицы умножить на это число: .

Пример 2.

.

При умножении матрицы на число справедливы следующие свойства: 1.) ; 2.) ; 3.) .

Умножение матриц

Произведением матрицы из строк и столбцов на матрицу из строк и столбцов, элемент который равен сумме произведений элементов -й строки матрицы на соответствующие элементы -го столбца матрицы , т.е.

.

Пример 3.

.

В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица множитель, т.е. . Так, произведение двух матриц 3-го порядка можно символически представить:

.

При умножении матрицы справедливы свойства:

1.) - переместительный закон не верен;

2.) ;

3.) ;

4.) ;

5.) ;

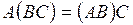6.) .

Обратная матрица

Определение: Матрица называется обратной для матрицы , если .

Теорема: Для того, чтобы квадратная матрица имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Нахождение матрицы, обратной данной:

Пусть дана невырожденная матрица

, .

Можно доказать, что обратная матрица определяется равенством: , (6)

где 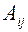есть алгебраическим дополнением элемента определителя матрицы .

Замечание: Элементами обратной матрицы являются алгебраические дополнения элементов транспонированной матрицы, деление на определитель матрицы.

Пример 4. Найти матрицу обратную данной: .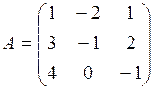

Решение: Воспользуемся формулой (6). Найдем определитель матрицы .

.

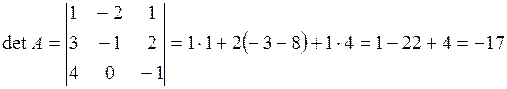Находим алгебраические дополнения:

; ; ;

; ; ;

; ; .

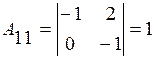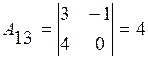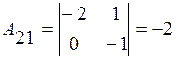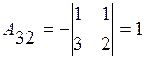Следовательно:

.

Ранг матрицы

Пусть дана матрица из строк и столбцов. Выделим в ней произвольно строк и столбцов (, ). Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу -го порядка. Определитель этой матрицы называется минором -го порядка матрицы .

Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы . Так, если ранг матрицы 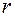, то это означает, что среди миноров порядка 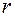есть хотя бы один минор, не равный нулю, а все миноры высшего порядка (чем 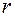) равны нулю.

При определении ранга матрицы приходится вычислять большое количество определителей. Чтобы облегчить этот процесс, используют специальные приёмы. Вначале введем понятие элементарных преобразований матрицы:

1.) умножение всех элементов какой-либо строки 9столбца) на число ;

2.) прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

3.) перемена местами строк (столбцов) матрицы;

4.) отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю;

Матрицы, полученные одна из другой при элементарных преобразованиях, называются эквивалентными. Эквивалентные матрицы имеют одинаковый ранг. .

Пример 5. Вычислить ранг матрицы

.

Решение: Используя элементарные преобразования получим:

. .

Так как минор второго порядка отличен от нуля, то .

Вопросы для самопроверки

Что называется матрицей? Как обозначается матрица и как определяется её размер?

Назовите виды матриц.

Как определяются линейные операции над матрицами и каковы их свойства?

Что называется произведением двух матриц? Каковы свойства произведений матриц?

Какая матрица называется обратной для данной матрицы? Всегда ли существует обратная матрица? Как можно найти обратную матрицу?

Что называется рангом матрицы и как его можно найти?

Не нашли, что искали? Воспользуйтесь поиском: