
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры для самостоятельного решения
Выполнит действия:
1.  ; 2.
; 2. 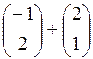 ;
;
3. 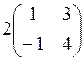 ; 4.
; 4.  ;
;
5. 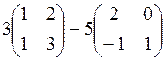 ; 6.
; 6. 
7.  8.
8. 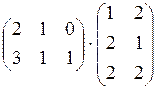 ;
;
9.  ; 10.
; 10.  .
.
11. Найти  , где
, где  ;
;
12. Найти  , где
, где  ;
;
13. Найти  , где
, где  ,
,  -единичная матрица
-единичная матрица
14. Найти  , при
, при  ;
;
15. Найти  , при
, при  ;
;
Найти обратную матрицу  , если
, если
16.  ; 17.
; 17.  ;
;
18.  ; 19.
; 19.  ;
;
Определить ранг матрицы  :
:
20.  ; 21.
; 21.  ;
;
22. 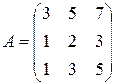 ; 23.
; 23.  .
.
Ответы к примерам
1.  ; 2.
; 2.  ; 3.
; 3.  ;
;
4.  ; 5.
; 5.  ; 6.
; 6. 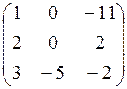 ;
;
7.  ; 8.
; 8.  ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14. 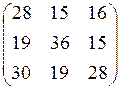 ; 15.
; 15. 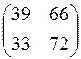 ;
;
16.  ; 17.
; 17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ; 23.
; 23.  .
.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Литература: (1, с. 18-34; 2, с. 82-100; 3, с. 286-275)
Основные понятия
Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.
В системе может быть любое число уравнений с любым числом неизвестных.
Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.
Система, имеющая решение, называется совместной, в противном случае – несовместной.
Для решения системы применяют различные методы.
3.2 Решение систем  линейных уравнений с
линейных уравнений с 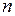 неизвестными
неизвестными
Пусть  (число уравнений равно числу неизвестных).
(число уравнений равно числу неизвестных).
Метод Крамера
Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:
 (7)
(7)
Для нахождения неизвестных  применим формулу Крамера:
применим формулу Крамера:
 (8)
(8)
где 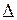 - определитель системы, элементы которого есть коэффициенты при неизвестных:
- определитель системы, элементы которого есть коэффициенты при неизвестных:
 .
.
 получается путём замены первого столбца определителя
получается путём замены первого столбца определителя 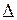 столбцом свободных членов:
столбцом свободных членов:
 .
.
Аналогично:
 ;
;  .
.
Пример 1. Решить систему по формуле Крамера:
 .
.
Решение: Воспользуемся формулами (8):
 ;
;
 ;
;
 ;
;
 ;
;
Тогда

Ответ:  .
.
Для любой системы 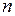 линейных уравнений с
линейных уравнений с 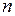 неизвестными можно утверждать:
неизвестными можно утверждать:
1) Если определить системы  , то система имеет единственное решение, которое может быть найдено по формулам Крамера.
, то система имеет единственное решение, которое может быть найдено по формулам Крамера.
2) Если 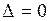 , то правило Крамера неприменимо. В этом случае система может иметь бесчисленное множество решений, если
, то правило Крамера неприменимо. В этом случае система может иметь бесчисленное множество решений, если  или не иметь их, если хотя бы один из определителей
или не иметь их, если хотя бы один из определителей  не равен нулю.
не равен нулю.
Матричный способ решения
Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.
Используя правила умножения матриц, данную систему уравнений можно записать в виде:  , где
, где
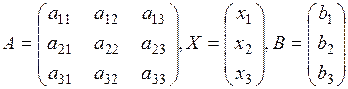 .
.
Пусть матрица  невырожденная, т.е.
невырожденная, т.е.  . Умножая обе части матричного уравнения слева на матрицу
. Умножая обе части матричного уравнения слева на матрицу  , обратную матрице
, обратную матрице  , получим:
, получим:  .
.
Учитывая, что  , имеем
, имеем
 (9)
(9)
Пример 2. Решить систему матричным способом:
 .
.
Решение: Введём матрицы:
 - из коэффициентов при неизвестных;
- из коэффициентов при неизвестных;
 - столбец свободных членов.
- столбец свободных членов.
Тогда систему можно записать матричным уравнением:  .
.
Воспользуемся формулой (9). Найдём обратную матрицу  по формуле (6):
по формуле (6):
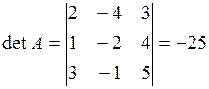 ;
;
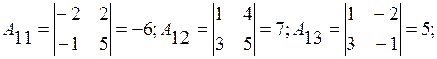


Тогда
 .
.
Следовательно,
 Получили:
Получили:
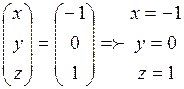 .
.
Ответ:  .
.
Метод последовательного исключения неизвестных (метод Гаусса)
Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:
 .
. 
Допустим, что  (если
(если 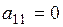 , то изменим порядок уравнений, выбрав первым уравнением то, в котором коэффициент при
, то изменим порядок уравнений, выбрав первым уравнением то, в котором коэффициент при 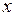 не равен нулю).
не равен нулю).
Первый шаг: а) делим уравнение  на
на  ; б) умножаем полученное уравнение на
; б) умножаем полученное уравнение на  и вычитаем из
и вычитаем из  ; в) затем полученное умножаем на
; в) затем полученное умножаем на  и вычитаем из
и вычитаем из  . В результате первого шага будем иметь систему:
. В результате первого шага будем иметь систему:


причём

 ,
,

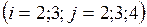
Второй шаг: поступаем с уравнением  и
и  точно так же, как с уравнениями
точно так же, как с уравнениями  .
.
В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.
Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.
Пример 3. Решить методом Гаусса систему:
 .
.
Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.
 ~
~  ~
~  ~
~  ~
~
~  .
.
По полученной матрице выписываем преобразованную систему:
 .
.
Тогда
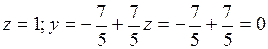

Ответ:  .
.
Замечание: Если система имеет единственное решение, то ступенчатая система приводится к треугольной, то есть к такой, в которой последнее уравнение будет содержать одно неизвестное. В случае неопределённой системы, то есть такой, в которой число неизвестных больше числа линейно независимых уравнений, треугольной системы не будет, так как последнее уравнение будет содержать более одного неизвестного (система имеет бесчисленное множество решений). Когда же система несовместна, то, после приведения её к ступенчатому виду, она будет содержать хотя бы одно 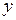 значение вида
значение вида  , то есть уравнение, в котором все неизвестные имеют нулевые коэффициенты, а правая часть отлична от нуля (система решений не имеет). Метод Гаусса применим к произвольной системе линейных уравнений (при любых
, то есть уравнение, в котором все неизвестные имеют нулевые коэффициенты, а правая часть отлична от нуля (система решений не имеет). Метод Гаусса применим к произвольной системе линейных уравнений (при любых  и
и  ).
).
Не нашли, что искали? Воспользуйтесь поиском: