
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теорема существования решения системы линейных уравнений
При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.
Пусть дана система  линейных уравнений с
линейных уравнений с 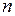 неизвестными:
неизвестными:
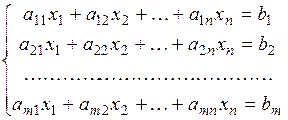 (10)
(10)
Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы
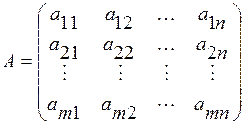 .
.
был равен рангу её расширенной матрицы
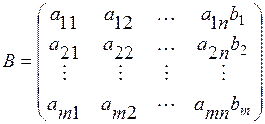 .
.
Причём, если  , то система (10) имеет единственное решение; если же
, то система (10) имеет единственное решение; если же 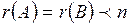 , то система имеет бесчисленное множество решений.
, то система имеет бесчисленное множество решений.
3.4 Линейная, однородная система 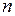 уравнений с
уравнений с 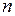 неизвестными
неизвестными
Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:
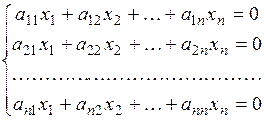 .
.
Эта система всегда совместна, так как она имеет нулевое решение 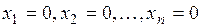 .
.
В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.
Терема. Для того, чтобы однородная система линейчатых уравнений имела нулевое решение, необходимо и достаточно, чтобы её определитель 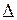 был равен нулю:
был равен нулю:
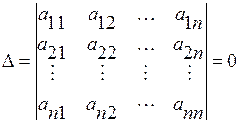 .
.
Таким образом, если  , то решение
, то решение 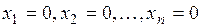 - единственное. Если
- единственное. Если 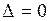 , то существует бесконечноё множество других ненулевых решений. Укажем один из способов отыскания решений для однородной системы трёх линейных уравнений с тремя неизвестными в случае
, то существует бесконечноё множество других ненулевых решений. Укажем один из способов отыскания решений для однородной системы трёх линейных уравнений с тремя неизвестными в случае 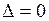 .
.
Можно доказать, что если 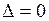 , а первое и второе уравнения непропорциональны (линейно независимы), то третье уравнение есть следствие первых двух. Решение однородной системы трёх уравнений с тремя неизвестными сводится к решению двух уравнений с тремя неизвестными. Появляется так называемое свободное неизвестное, которому можно придавать произвольные значения.
, а первое и второе уравнения непропорциональны (линейно независимы), то третье уравнение есть следствие первых двух. Решение однородной системы трёх уравнений с тремя неизвестными сводится к решению двух уравнений с тремя неизвестными. Появляется так называемое свободное неизвестное, которому можно придавать произвольные значения.
Пример 4. Найти все решения системы:
 .
.
Решение. Определитель этой системы
 .
.
Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:
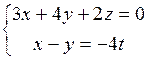 .
.
Полагая, например,  , получим
, получим
 .
.
Решая систему двух линейных уравнений, выразим 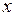 и
и 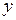 через
через 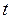 :
: 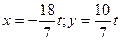 . Следовательно, решение системы можно записать в виде:
. Следовательно, решение системы можно записать в виде: 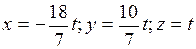 , где
, где 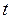 - произвольное число.
- произвольное число.
Пример 5. Найти все решения системы:
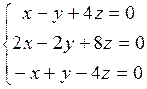 .
.
Решение. Нетрудно видеть, что в данной системе только одно независимое уравнение (два других ему пропорциональны). Система из трёх уравнений с тремя неизвестными свелась к одному уравнению с тремя неизвестными. Появляются два свободных неизвестных. Найдя, например, из первого уравнения  при произвольных
при произвольных 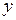 и
и  , получим решения данной системы. Общих вид решения можно записать
, получим решения данной системы. Общих вид решения можно записать 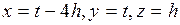 , где
, где 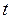 и
и 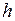 - произвольные числа.
- произвольные числа.
Вопросы для самопроверки
Сформулируйте правило Крамера для решения системы 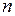 линейных уравнений с
линейных уравнений с 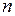 неизвестными.
неизвестными.
В чём сущность матричного способа решения систем?
В чём заключается метод Гаусса решения системы линейных уравнений?
Сформулируйте теорему Кронекера-Капелли.
Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.
Не нашли, что искали? Воспользуйтесь поиском: