Область D, правильная в направлении оси оy

Такая область ограничена сверху линией 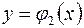, снизу – линией , функци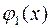и и непрерывны, слева и справа - соответственно отрезками прямых , (рис. 1). В частных случаях один из этих отрезков (или оба вместе) может превратиться в точку (рис. 2). При этом всякая прямая, параллельная оси оy и проходящая внутри отрезка , пересекает нижнюю и верхнюю границы только в одной точке.

Рис. 1 Рис. 2

Область определяется неравенствами вида

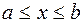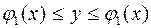, . (2)

Двойной интеграл по области, правильной в направлении оси оу, вычисляется по формуле

. (3)

Здесь по переменной у берется внутренний интеграл ,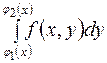
х считается постоянной величиной. В результате получается некоторая функция от х, которая интегрируется затем от а до b. Таким образом, вычисление двойного интеграла (3) сводится к последовательному вычислению двух определенных интегралов.

Не нашли, что искали? Воспользуйтесь поиском: