Основные свойства двойного интеграла

Свойство 1. 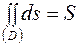или , где – площадь области .

Свойство 2. Постоянный множитель можно выносить за знак двойного интеграла:

.

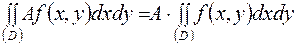Свойство 3. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от слагаемых функций:

.

Свойство 4. Если область разбить линией на две части и , то

.

Свойство 5. Если в области , то .

Свойство 6. Если в области , то

.

Свойство 7. Есл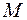и и соответственно наибольшее и наименьшее значения в области , то

,

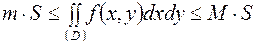где – площадь области .

Свойство 8. Если функция непрерывна в ограниченной замкнутой области с площадью , то в ней найдется такая точка , что двойной интеграл

.

Примечания:

1. Доказательства свойств двойного интеграла проводятся аналогично доказательствам соответствующих свойств определенного интеграла.

2. Если верхняя или нижняя граница области , рассматриваемой в направлении оси , или обе ее границы на разных участках отрезка заданы различными уравнениями, то область разбивают на части, правильные в направлении оси . Каждая из них будет ограничена сверху только одной кривой, заданной на соответствующем участке отрезка одним уравнением. Снизу – тоже только одной кривой. Интеграл по области будет представлен суммой интегралов по получившимся областям (применяется четвертое свойство двойных интегралов).

Аналогично поступают и в случае, когда левая или правая граница области D, рассматриваемой в направлении оси , или обе ее границы на разных участках отрезка заданы различными уравнениями.

Не нашли, что искали? Воспользуйтесь поиском: