Вычисление двойного интеграла в полярной системе

Координат

Формулы для вычисления двойного интеграла в прямоугольной системе координат получены для областей, правильных в направлении оси oy или ox. Любую замкнутую область можно разбить на правильные области и данный интеграл по области представить в виде суммы интегралов по этим областям, затем для их вычисления применить первое или второе правило. Однако для некоторых видов областей вычисление двойных интегралов упрощается, если применять другие системы координат, например полярную.

Определение. Область D называется правильной в полярной системе координат, если она ограничена двумя лучами 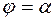, , 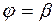исходящими из начала координат, и двумя линиями 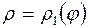, , 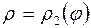где 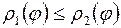. Функции 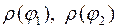– непрерывные на отрезке .

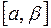Если граница области D проходит через начало координат или начало координат лежит в области D, то 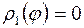(рис. 8).

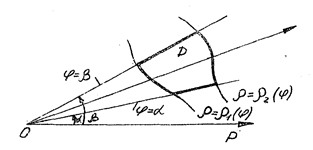
Рис. 8

Область D определяется неравенствами вида:

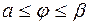, . (6)

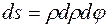– в полярной системе координат. Так как декартовы и полярные координаты связаны формулами 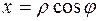, , 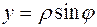то

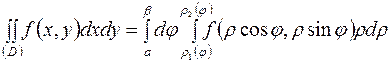. (7)

Как и в прямоугольной системе координат, внутренний интеграл формулы (7) берется по 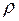, 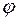считается постоянной. Затем полученный результат надо проинтегрировать по 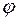в пределах от 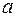до .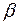

Примечания:

1. При расстановке пределов интегрирования в двойном интеграле по области D, правильной в полярной системе координат, проводят через область D луч-стрелку, выходящую из точки 0. Первую линию, которую пересекает стрелка, называют линией входа, а вторую – линией выхода (см. рис. 8) из области.

2. К полярным координатам целесообразно переходить, когда
подынтегральная функция или уравнения границ области содержат выражение . Тогда .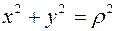

Не нашли, что искали? Воспользуйтесь поиском: