Изменение порядка интегрирования в двойном интеграле

Сведение двойного интеграла к повторному (двукратному) по формуле (3) или (5) еще называют расстановкой пределов интегрирования по области D. Таким образом, два основных вида области D в прямоугольной системе координат дают два правила расстановки пределов интегрирования в двойном интеграле.

В некоторых задачах пределы интегрирования в двойном интеграле расставлены по одному какому-нибудь правилу, а требуется расставить их по другому правилу (в таком случае говорят: изменить порядок интегрирования). Для решения задачи нужно сначала по данному интегралу восстановить область интегрирования, а затем расставить пределы интегрирования по другому правилу. Для восстанов-ления области интегрирования D нужно:

1) найти уравнения линий, ограничивающих область D (они получаются, если приравнять пределы интегрирования во внутреннем и внешнем интегралах тем переменным, по которым проводится интегрирование);

2) построив эти линии, получить область D.

Задача 1.31 [10]

Изменить порядок интегрирования:

.

Литература: [5, гл. 8, § 1], [7, гл. 7, § 1], [9, гл. 10, § 1].

Решение:

К переменной y приравняем пределы интегрирования во внутренних интегралах, к переменной х – во внешних.

, , , , , .

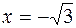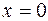Получили уравнения линий, ограничивающих область D. Построив эти линии, восстановим область. Для этого преобразуем второе и третье уравнения: 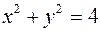, 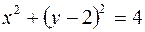– это окружности, 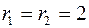. Точки (0, 0), (0, 2) – их центры. – верхняя половина окружности , 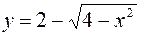– нижняя половина второй окружности (рис. 5).

Область – криволинейный треугольник AOB.

Решая систему уравнений , получим точку пересечения двух окружностей, принадлежащую области .

Рис. 5

В задаче пределы интегрирования в двойном интеграле расставлены по первому правилу. Изменение порядка интегрирования означает расстановку пределов по второму правилу.

Уравнения нижней и верхней прямых, ограничивающих об-
ласть :

, ; – линия входа, AO – линия выхода.

Найдем из уравнений первой и второй окружностей:

– дуга , – дуга AO. Перед радикалами взят знак «минус», так как дуги окружностей распо­ложены в левой полуплоскости. Тогда неравенства (4) примут вид:

, .

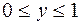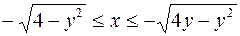Вместо суммы двух интегралов в ответе будет один двойной интеграл, так как слева область D ограничена одной кривой , справа – тоже одной кривой .

Ответ: .

2.1.4 Вычисление двойного интеграла в прямоугольной системе
координат

Задачи на вычисление двойного интеграла в прямоугольной системе координат решаются по формуле (3) или (5). Для этого вначале надо установить, какой из внутренних интегралов вычисляется проще:

или ,

а затем выяснить, нужно ли разбивать область D на части, т.е. выбирают первое или второе правило. Умение выбирать подходящее правило вырабатывается в процессе решения задач, и мы покажем, как это делается.

Задача 2.31 [10]

Вычислить .

.

Литература: [5, гл. 8, § 1], [6, гл. 1, § 1], [7, гл. 7, § 1], [9, гл. 10,
§ 1].

Решение:

Построим область D (рис. 6): – прямая, – кубическая парабола, – ветвь параболы , расположенная в нижней полуплоскости. Область D – криволинейный треугольник OAB.

Рис. 6

Внутренние интегралы формул (3) и (5) легко вычисляются. Применяя первое правило, область интегрирования ОАВ не нужно разбивать на части. По второму правилу следует разбивать ОАВ на две области – OAC и OCB, так как линия входа ОАВ в направлении оси ох состоит из двух различных кривых: – дуга , – дуга . Поэтому для вычисления двойного интеграла здесь лучше применить первое правило.

Неравенства (2) принимают вид: , .

По формуле (3)

Проверьте результат, решив задачу по второму правилу.

Задача 3.31 [10]

Вычислить .

.

Решение:

Построим область (рис. 7): D – прямоугольник, который является областью, правильной и в направлении оси оy, и в направлении оси ох. Здесь лучше применить второе правило, так как вычисляется проще, чем 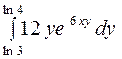(во втором случае требуется интегрирование по частям, тогда как в первом – вычисление с помощью табличного интеграла).

Рис. 7

По формуле (5)

Не нашли, что искали? Воспользуйтесь поиском: