Вычисление массы неоднородной плоской фигуры

Если неоднородная фигура имеет плотность 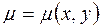, где – функция, непрерывная в области , то масса фигуры вычисляется по формулам:

в прямоугольной системе координат

; (10)

в полярной системе координат

(11)

Задача 8.31 [10]

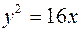
Пластинка задана ограничивающими ее кривыми: , , 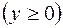; – поверхностная плотность. Найти массу пластинки.

Литература: [5, гл. 8, § 1], [6, т. 2, гл. 1, § 6], [7, гл. 7, § 5], [8, гл. 7, § 6], [9, гл. 10, § 6].

Решение:

Воспользуемся формулой (10):

т.е. получили задачу, аналогичную задаче 2.31.

Построим область (рис. 11): пластинка – область, правильная в направлении оси oy и оси ox. B (1/4, 2), внутренние интегралы формул (3) и (5) легко вычисляются.

Рис. 11

По первому правилу вычисления двойного интеграла нера-
венства (2) примут вид:

, .

Если же применить второе правило, то неравенства (4) принимают вид:

, .

Воспользуемся вторым правилом. По формуле (5)

Проверьте результат, найдя массу пластинки по первому правилу.

Задача 9.31 [10]

Пластинка задана неравенствами: , , ; – поверхностная плотность. Найти массу пластинки.

Решение:

Из двойного неравенства видно, что фигура ограничена кривыми с уравнениями:

, .

Это эллипсы, центры которых находятся в начале координат. У первого из них полуоси , ; у второго эллипса полуоси , . Построим область D (рис. 12).

Рис. 12

Пластинка D – область – является правильной в полярной системе координат (см. рис. 8), но вычисление массы m по формуле (11) более сложно, чем по формуле (10). Таким образом, будем вычислять двойные интегралы в прямоугольной системе координат. Если пользоваться первым правилом, то область D надо разбить вертикалью через точку N на две области. Согласно второму правилу область нужно будет разбить на три части горизонталями через точки А и М. Поэтому применим первое правило (оно дает два двойных интеграла).

Найдем абсциссы точек пересечения 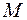и прямой с обоими эллипсами, решая системы уравнений:

Из первой получаем , , абсцисса точки равна . Из второй: , 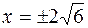. Абсцисса точки 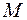равна . Таким образом, неравенства (2) для областей и примут соответственно вид:

, , , .

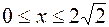С помощью второго правила нужно будет вычислять три двойных интеграла, при этом определенные интегралы приводятся к интегралам от рациональных функций и, следовательно, до конца интегрируются, как и по первому правилу (проверьте это самостоятельно).

Не нашли, что искали? Воспользуйтесь поиском: