Вычисление тройных интегралов в декартовой системе

Координат

Чтобы вычислить тройной интеграл по области (V), правильной в направлении оси oz, нужно:

1) найти проекцию области (V) на плоскость xoy, т.е. найти область D;

2) найти уравнения нижней и верхней поверхностей, ограничивающих область (V), т.е. , ;

3) проинтегрировать функцию по z в пределах от до , считая x и y постоянными;

4) полученный результат проинтегрировать по области D.

Таким образом, тройной интеграл вычисляют в декартовой системе координат по одной из формул:

, (14)

когда область D является правильной в направлении оси oy;

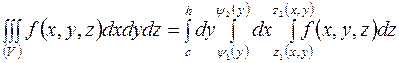, (15)

когда область является правильной в направлении оси ox. Эти формулы получаются, если тройной интеграл представить в виде:

. (16)

Следует обратить внимание на то, что формулы (14) и (15) являются как бы «продолжением» формул (3) и (5).

Примечание. В задачах типового расчёта «Кратные интегралы» часто область (V) проектируется на плоскость xoy. При вычислении тройного интеграла, когда проекция области (V) принадлежит плоскости xoz или yoz, формулы (14), (15), (16) принимают аналогичный вид.

Задача 4.31 [10]

Вычислить .

V: x = 2, , , , .

Литература: [5, гл. 8, § 2], [6, т. 2, гл. 1, § 7], [7, гл. 7, § 6], [9,
гл. 10, § 7].

Решение:

Построим область (V) (рис.15).

OAB – проекция тела на плоскость xoy, область D (рис.16).

Рис. 15 Рис. 16

Треугольная призма – область (V) – является правильной областью в направлении всех трех осей. , – это уравнения нижней и верхней плоскостей (поверхности входа в область (V) и выхода).

.

Таким образом, пришли к задаче, аналогичной задаче 3.31. Интеграл вычисляется проще, чем интеграл . Значит, надо применять первое правило – формулу (3): , .

Задача 5.31 [10]

Вычислить .

V: , , , , .

Решение:

Построим проекцию области (V) (рис. 17). Пределы интегрирования определим по уравнениям поверхностей: , , .

Рис. 17

Как и в задаче 4.31, область (V) является правильной в направлении всех трех осей. Поверхность входа – плоскость z = 0, выхода – гиперболический параболоид z = xy. Тогда

,

пришли к задаче, аналогичной задаче 2.31.

Внутренние интегралы формул (3) и (5) легко вычисляются. Применим, например, первое правило для вычисления полученного двойного интеграла.

Не нашли, что искали? Воспользуйтесь поиском: