Вычисление объемов с помощью тройных интегралов

В прямоугольной системе координат формула для вычисления объема тела имеет вид:

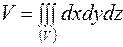; (19)

в цилиндрических координатах:

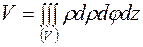; (20)

в сферических координатах:

. (21)

Задача 11.31 [10]

Найти объем тела, заданного ограничивающими его поверхностями: , , .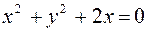

Решение:

Первое уравнение 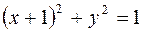– круговой цилиндр, ось цилиндра параллельна оси oz и проходит через точку (–1, 0, 0). Второе уравнение определяет параболический цилиндр. Построим тело
(рис. 20) и его проекцию (рис. 21). Проекция области (V) на плоскость xoy представляет круг с центром в точке (–1, 0), 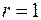. По прямым 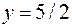, параболический цилиндр пересекается с плоскостью xoy.

Рис. 20

Из уравнений , получаем 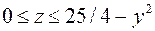. По формуле (19)

.

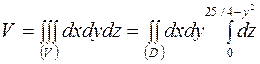Круговой цилиндр содержит выражение 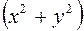, тогда для вычисления двойного интеграла целесообразно перейти от прямоугольных координат к полярным, т.е. объем тела проще вычислять не по формуле (19), а по формуле (20) в цилиндрических координатах.

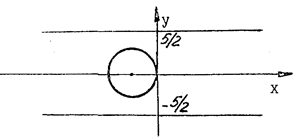
Рис. 21

Полагая в уравнении 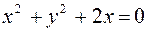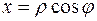, , 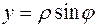получим 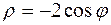. Это уравнение окружности в полярных координатах. Так как эта окружность проходит через начало координат, то в неравенствах (6) . Эти неравенства примут вид (см. рис. 20
и 21):

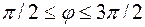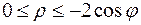, и .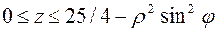

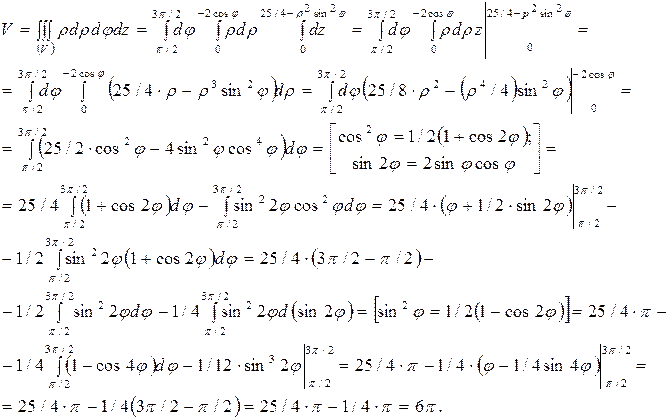
Задача 12.31 [10]

Найти объем тела, заданного ограничивающими его поверхностями: , , , .

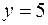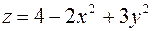Решение:

Уравнение определяет параболический цилиндр, направляющей которого является парабола с вершиной в точке (0, 7), а образующая параллельна оси oz. Ветви параболы направлены вниз, симметрично оси oy. Третье и четвертое уравнения определяют гиперболические параболоиды. Они ограничивают тело снизу и сверху. Построим проекцию тела на плоскость xoy (рис. 22).

Рис. 22

Фигура ABC – область D: A (–1, 5), B (0, 7), C (1, 5) Гиперболические параболоиды не пересекают границу области ABC. Объем тела проще вычислять в прямоугольной системе координат.

Для вычисления двойного интеграла следует применить первое правило, тогда пределы переменных x и y будут содержать рациональные выражения. Действительно, неравенства (2) принимают вид: , 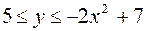. По уравнениям гиперболоидов получим: .

Задача 13.31 [10]

Найти объем тела, заданного ограничивающими его поверхностями: , .

Решение:

Первое уравнение определяет верхнюю половину сферы 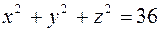, второе – верхнюю часть конуса 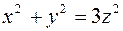. Построим область (V) (рис. 23).

Найдем линию пересечения заданных поверхностей, приравнивая правые части их уравнений:

, ,

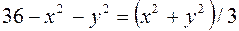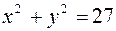
Получили окружность с центром в начале координат, .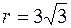

Рис. 23 Рис. 24

Круг радиусом является проекцией тела (рис. 24). Объем тела проще находить по формуле (20), т.е. в цилиндрических координатах (указание, что уравнения границ области (V) содержат выражение 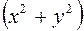, выполнено). Область (V) является правильной в направлении оси oz, и ее не надо разбивать на части. По уравнениям поверхностей получим:

.

Из уравнения окружности 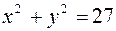следует:

, .

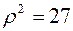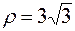
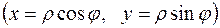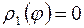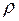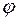, так как начало координат лежит в области D. Неравенства (6), определяющие пределы переменных и цилиндрической системы координат, принимают вид (см. рис. 23 и 24):

, .

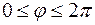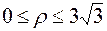Тогда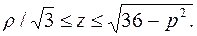

В полученном двойном интеграле вычислим отдельно внутренний интеграл.

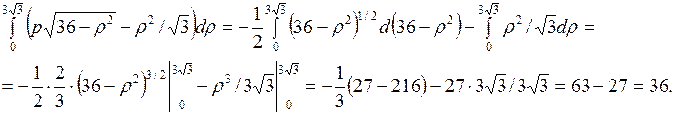
Тогда

.

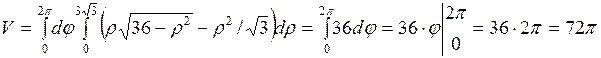Задача 14.31 [10]

Найти объем тела, заданного ограничивающими его поверхностями:

, .

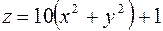Решение:

Первое уравнение определяет параболоид вращения, второе – плоскость, параллельную оси ox (рис. 25). Приравняем их правые части, чтобы найти уравнение линии пересечения этих поверхностей.

, , .

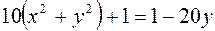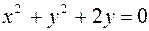Получили окружность с центром в точке (0, –1), r = 1. Круг 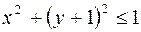является проекцией тела (рис. 26).

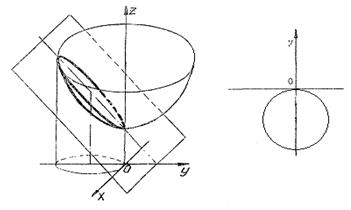
Рис. 25 Рис. 26

Далее поступим, как и в предыдущей задаче. Объем тела будем вычислять с помощью формулы (20) в цилиндрических координатах, , .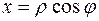

Тогда поверхность входа ;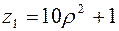

поверхность выхода ; .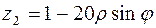

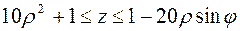Уравнение окружности 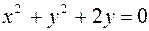в полярных (цилиндрических) координатах имеет вид: .

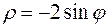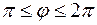; (см. рис. 26).

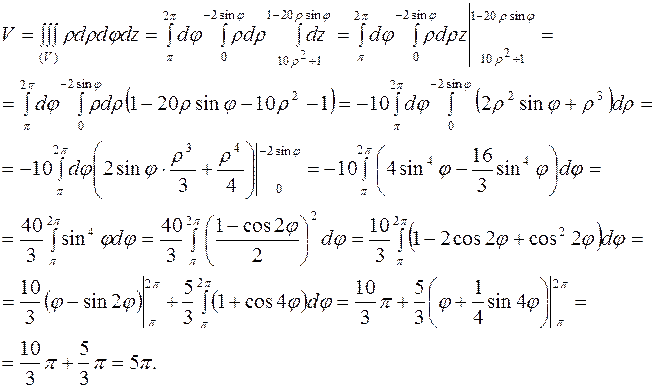
Задача 15.31 [10]

Найти объем тела, заданного неравенствами:

, , , .

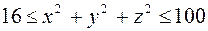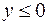Решение:

Область (V) ограничена двумя сферами (, 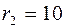), плоскостью xoy, верхней частью конуса , плоскостью zox и плоскостью 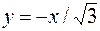(рис. 27). Найдем уравнение линии пересечения конуса и сферы 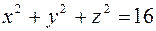, решая систему уравнений:

, , , .

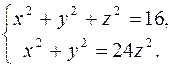
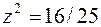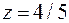Получили окружность с центром в начале координат, .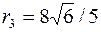

Построим проекцию тела на плоскость xoy (рис. 28).

Область ABCE – область D.

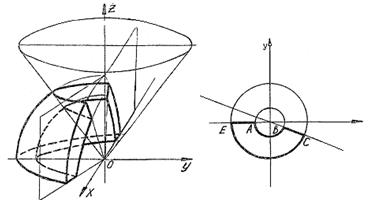
Рис. 27 Рис. 28

Уравнения границ области (V) содержат выражения (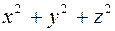), . Это указывает на целесообразность вычисления объема тела в сферических координатах. Действительно, в направлении 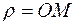(см. рис. 19) область (V) будет правильной в сферической системе координат, ее не надо разбивать на части, следовательно, будет один тройной интеграл.

Для цилиндрических и декартовых координат область (V) нужно разбивать на три части, правильные в направлении оси oz. Это хорошо видно из рис. 29, на котором представлено сечение тела плоскостью zoy. Следовательно, в этих координатах объем тела представляет сумму трех тройных интегралов (для декартовых координат добавляется еще и сложность вычисления определенных интегралов).

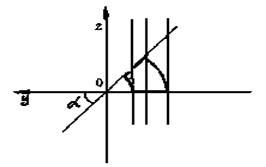
Рис. 29

Таким образом, отпадает вариант решения задачи по формулам (19) и (20). (Нужно ясно понимать, когда область правильная не только на плоскости xoy, но и в других координатах: полярных, цилиндрических, сферических.)

Найдем пределы для переменных , , .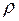

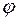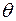Так как , то 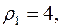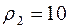, т.е. .

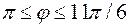(см. рис. 27, 28).

Для нахождения пределов переменной 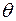обратимся к рис. 30.

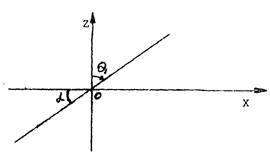
Рис. 30

Конус 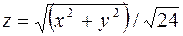получится, если вращать прямую 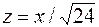вокруг оси oz, , , .

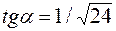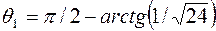Тогда .

Вычислим отдельно внутренний интеграл.

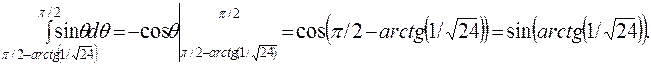
Далее воспользуемся формулами, связывающими обратные тригонометрические функции:

, .

.

.

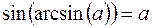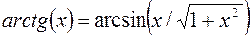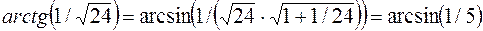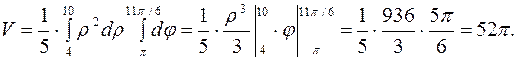
Не нашли, что искали? Воспользуйтесь поиском: