Вычисление массы неоднородного тела

Если неоднородное тело имеет плотность , где – функция, непрерывная в области (V), то масса тела вычисляется по следующим формулам:

в прямоугольной системе координат

; (22)

в цилиндрической системе координат

; (23)

в сферической системе координат

. (24)

Вычисление массы неоднородного тела с помощью тройного интеграла аналогично вычислению массы неоднородной фигуры с помощью двойного интеграла. Это видно, если сравнить формулы (22) – (24) и (10), (11).

Задача 16.31 [10]

Тело V задано ограничивающими его поверхностями, – плотность. Найти массу тела: , , , , .

Решение:

Построим тело (рис. 31) и его проекцию на плоскость xoy
(рис. 32).

Рис. 31 Рис. 32

Первое уравнение определяет конус с вершиной в начале координат, второе – цилиндр с осью oz. Проекцией тела является полукруг , расположенный в верхней полуплоскости . В данных задачи три уравнения содержат выражение 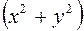. Поэтому сделаем переход в тройном интеграле от декартовых координат к цилиндрическим.

, .

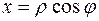Тогда , , , ; .

Область (V) является правильной в направлении оси oz.

Для определения пределов переменных 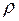и 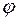воспользуемся неравенствами (6). , 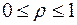(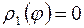, так как прямая AB области D проходит через начало координат) (см. рис. 32).

По формуле (23)

Вопросы для самопроверки

Двойной интеграл

1. Что называется двойным интегралом от функции f (x, y) по области D? Каков его геометрический смысл?

2. Сформулируйте свойства двойного интеграла.

3. Как вычисляется двойной интеграл от функции f (x, y) по области D?

4. Обоснуйте формулы, служащие для вычисления объема цилиндрического тела, площади плоской фигуры и ее массы с помощью двойных интегралов.

5. Получите формулу для вычисления двойного интеграла в полярных координатах.

Тройной интеграл

1. Что называется тройным интегралом от функции f (x, y, z) по пространственной области (V)? Каков его механический смысл?

2. Сформулируйте свойства тройного интеграла.

3. Как свести тройной интеграл от функции f (x, y, z) по правильной области (V) в направлении оси oz к трехкратному?

4. Каковы правила перехода в тройном интеграле к сферическим координатам?

5. Как вычисляется тройной интеграл в цилиндрических координатах?

6. Как вычисляется объем тела с помощью тройного интеграла?

Список рекомендуемой литературы

1. Бугров Я.С. Дифференциальные уравнения. Кратные интегралы и др. / Я.С. Бугров, С.М. Никольский.– М.: Наука, 1985.

2. Кудрявцев Л.Д. Курс математического анализа. Т. 2. – М.: Высшая школа, 1988.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 2. – М.: Наука, 1978.

4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 3. – М.: Физматгиз, 1963.

5. Сборник задач по математике для втузов. Специальные разделы математического анализа. /Под ред. А.В. Ефимова, Б.П. Демидовича.– М.: Наука, 1986.

6. Данко П.Е. Высшая математика в упражнениях и задачах /
П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Наука, 1986.

7. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1964.

8. Сборник задач по математическому анализу /Под ред. Б.П. Де-мидовича.– М.: Наука, 1978.

9. Сборник задач по курсу высшей математики / Под ред. Г.И. Кручковича.– М.: Высшая школа, 1965.

10. Кузнецов Л.А. Сборник заданий по высшей математике (ТР).– М.: Высшая школа, 1983.

11. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов/ И.Н. Бронштейн, К.А. Семендяев.– М.: Наука, 1982.

Учебное издание

Бородин Николай Павлович

Жернова Варвара Викторовна

Корнеева Елена Николаевна

Шоркин Владимир Сергеевич

Кратные интегралы

Учебно-методическое пособие

Редактор Т.Д. Васильева

Технический редактор Т.П. Прокудина

Орловский государственный технический университет

Лицензия ИД № 00670 от 05.01.2000

Подписано к печати 02. 09.2004 г. Формат 60 x 84 1/16.

Печать офсетная. Уч.-изд. л. 2,2. Усл. печ. л. 2,8. Тираж 500 экз.

Заказ №____

Отпечатано с готового оригинал-макета

на полиграфической базе ОрелГТУ,

302030, г. Орел, ул. Московская, 65.

Не нашли, что искали? Воспользуйтесь поиском: