Исчисление высказываний (ИВ).

Исчисление высказываний как формальную теорию можно определить с помощью аксиоматического метода, который характеризуется следующими тремя частями:

1. Явная формулировка исходных аксиом той или иной теории.

2. Явная формулировка правил вывода, используемых для последователь­ного построения этой теории.

3. Использование искусственно построенных формальных языков для изло­жения всех теорем рассматриваемой теории.

В понятие исчисления входят такие компоненты, как формальный язык исчисления, аксиомы исчисления и правила вывода. Они позволяют дать строгое математическое определение понятия доказательства и получить точные утверждения о возможности или невозможности доказательства тех или иных предложений теории.

В любом исчислении различают синтаксические и семантические вопросы исчисления. В синтаксической части изучают понятие доказательства (теория Доказательств), в семантической — структуру формальных языков (теория моделей).

Исчисления позволяют формализовать многие разделы математики и других наук. Исчисление высказываний — это аксиоматическая логическая система, описывающая тождественно истинные схемы, а ее интерпретация — алгебра высказываний.

Под алфавитом ИВ будем понимать:

1. Счетное множество символов 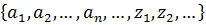- основные символы (буквы) алфавита;

2. Множество связок - логические символы;

3. Скобки (,) – вспомогательные символы.

Формулу ИВ определим следующим образом:

1) все буквы являются формулами;

2) если а и b формулы, то формулами будут являться

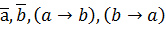
3) других формул нет.

Аксиомы ИВ:

А1. ;

A2. ;

A3. .

Правила вывода:

1. Правило подстановки: если известно, что некоторая формула ИВ, зависящая от букв является доказуемой, т.е. теоремой, то ее доказуемость сохранится в случае, если вместо букв подставить любую формулу ИВ.

2. Правило заключения (modus ponens): если доказуемой является формула , то доказуемой будет являться также формула В (или в виде функции вида: f (A, A

Выводом в теории будем называть всякую конечную последовательность формул, каждая из которых является либо аксиомой, либо получена из предыдущих формул по правилам вывода, при этом формулу называют выводимой формулой с использованием вывода длины n-1.

Доказуемые формулы обозначают

Формула ИВ называется доказуемой или теоремой, если существует вывод, оканчивающийся этой формулой, причем каждая формула вывода может быть:

1) аксиомой

2) доказуемой (теоремой);

3) получена из предыдущих по правилам вывода.

Правило силлогизма. Если доказуемы формулы и В , то доказуема формула , т.е. .

Не нашли, что искали? Воспользуйтесь поиском: