Мощность множества.

Понятие мощности множеств введено основателем теории множеств

Г. Кантором (1878), который установил, что мощность множества действительных чисел с больше À₀, и тем самым показал, что бесконечные множества могут быть расклассифицированы по их мощности.

Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком. Например, множество планет Солнечной системы U = {Земля, Марс, Вене­ра, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}. Заме­тим, что понятие универсального множества четко не определе­но, т. е. некорректно. U можно включить в другое множество W, и оно тоже будет универсальным. Например, долго считалось, что множество действительных чисел М универсально (т. е. описывает всю математику), пока не открыли поле комплексных чисел С и надкомплексные числа и не поняли, что не существует универ­сального числового множества. Тем не менее там, где область объек­тов не выходит за рамки некоего множества, иногда бывает удоб­но оперировать с этим термином. Ведь ржаное поле — вселенная для мыши.

Равными называют два множества А и В, состоящие из одина­ковых элементов: А = В. Например, равны множества решений уравнений 4х - 8 = 16, х/15 = 2/5 и 5^Х-3 = 125, так как их решением является одно и то же число 6.

Равны множества букв, из которых составлены слова «навес» и «весна». Равны множества корней уравнения х² = 1 и множество М = {(-1)^k, k = 0, 1, 2,...}. Поэтому задача «решить уравнение», знакомая с детства, в реальности означает «решить уравнение в каком-то множестве». Так, уравнение х² + 1 = 0 не имеет действи­тельных корней: {х| х² + 1 = 0, х М} = 0, но имеет два комплекс­ных корня х = i, х = - i: {х|х² + 1 = 0, х С} = { i, -i }.

Равенство двух множеств А и В означает также, что А В и В А. И наоборот, выполнение свойств A В и В А означает выполнение равенства А = В. Эти утверждения равносильны.

Число элементов множества А называется мощностью множе­ства и обозначается | А| или п(А). Так, мощность пустого множе­ства равна 0:

n() = 0, а мощность множества планет Солнечной системы n(U) = 9 или

|U| = 9.

Следующая формула позволяет найти мощность объединения нескольких множеств, если известны мощности каждого из них, а также мощности всех пересечений.

Формула включений и исключений:

|A |

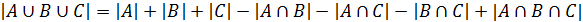
Множество состоит из букв латинского алфавита. Заданы множества A, B, C и D. Вычислить мощность множества X и Y.

1.1.

1.2.

1.3.

1.4.

1.5.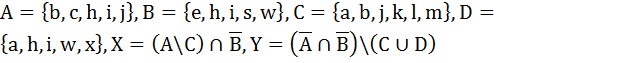

1.6.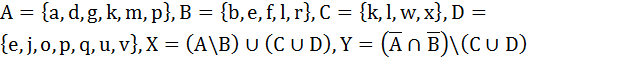

1.7.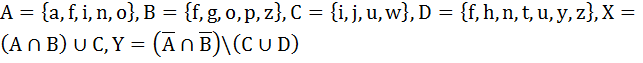

1.8. .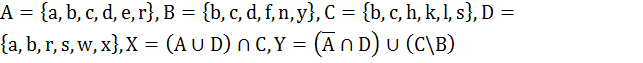

Отношения

Чтобы задать соответствие R между множествами X и Y, достаточно указать подмножество Г декартова произведения

При этом множество X называется областью отправления соответствия R, множество Y – областью прибытия, а множество Г – графиком соответствия R. Например, е сли R-соответствие «х нацело делится на у» и

.

Между двумя любыми множествами X и Y всегда существует полное (если график Г соответствия R совпадает со всем декартовым произведением X×Y) и пустое (если ) соответствия. Если задано соответствие xRy между множествами X и Y, то обратным ему называется соответствие ySx между множествами Y и X, такое что ySx существует в том и только том случае, когда xRy. В этом случае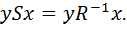

Бинарные соответствия между Х и Х называются бинарными отношениями на множестве Х. Отношение на множестве Х задано. Если указано множество Г: 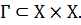Рассмотрим, например, на множестве отношение «х>y». График этого отношения – множество

Пусть на множестве Х задано бинарное отношение R. Тогда R называется рефлексивным, если . Отношение R называется антирефлексивным, если ни один элемент не находится в отношении R с самим собой.

Отношение R называется симметричным, если для любых элементов x и y из xRy следует yRx. Отношение R называется асимметричным, если ни для каких элементов x и y из множества Х не выполняется одновременно и xRy, и yRx. Отношение R называется антисимметричным, если xRy и yRx одновременно выполняются в том и только том случае, когда x=y.

Отношение R называется транзитивным, если для любых элементов x, y, z из множества Х из того, что xRy и yRz следует, что xRz.

Если отношение R в множестве Х обладает свойствами рефлексивности, симметричности и транзитивности, то оно называется отношением эквивалентности.

Отношение параллельности в множестве прямых на плоскости рефлексивно, симметрично и транзитивно. Это отношение разбивает множество всех прямых плоскости на классы, состоящие из параллельных друг другу прямых (пучки параллельных прямых).

Система непустых подмножеств множества Х называется разбиением, если каждый элемент из Х принадлежит одному и только одному подмножеству системы. Подмножества, входящие в разбиение, называются смежными классами разбиения.

Множество смежных классов разбиения ∑ множества Х называется фактор-множеством Х по разбиению ∑ и обозначается Х/∑.

Отношение R на множестве Х называется отношением строгого порядка, если оно транзитивно и асимметрично.

Отношение R на множестве Х называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.

Множество Х, на котором задано отношение порядка R (строго или нестрого), называется частично упорядоченным множеством. Например, множество Х= {3, 1, 5, 2,4} можно упорядочить с помощью отношения «х<y» или «x≤y».

Задания. Является ли отношение R на множестве М отношением эквивалентности? Отношением порядка? Какими свойствами обладает?

1.1.

1.2.

1.3.

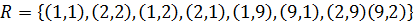
1.4.

1.5.

1.6.

1.7.

1.8.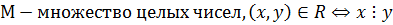

1.9.

1.10. .

Не нашли, что искали? Воспользуйтесь поиском: