Алгоритм представления логической функции, заданной таблицей, формулой в СКНФ

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Шаг 1. Выбираем в таблице все наборы переменных A ₁, A ₂,..., A_n, для которых значение F равно 0.

Шаг 2. Для каждого такого набора (строки таблицы) составляем дизъюнкцию переменных, причем в эту дизъюнкцию переменная A_i записывается без изменений (т. е A_i), если ее значение равно «0» и со знаком отрицания (т.е. ), если ее значение равно «1».

Шаг 3. Составляем конъюнкцию всех полученных дизъюнкций. В результате получится формула данной функции в СКНФ.

Формула называется тождественно-истинной (тавтологией), если для любых наборов переменных она принимает значение 1.

Формула называется тождественно-ложной, если для любых наборов переменных она принимает значение 0.

Формула называется выполнимой, если для некоторых наборов переменных она принимает значение 1.

Проблема разрешимости для логики высказываний заключается в том, чтобы установить, является ли произвольная формула тождественно-истинной.

Теорема. Формула является тождественно-истинной тогда и только тогда, когда в ее КНФ в любую из элементарных дизъюнкций одновременно входят какая-либо переменная и ее отрицание.

Теорема. Формула является тождественно-ложной тогда и только тогда, когда в ее ДНФ в любую из элементарных конъюнкций одновременно входят какая-либо переменная и ее отрицание.

Задания:

1. Построить СДНФ для функции f(x, y, z) = 01110110

2. Построить СКНФ для функции f(x, y, z) = 01100010

3. Построить СДНФ для функции f(x, y, z) = 01010010

4. Построить СКНФ для функции f(x, y, z) = 00110011

5. Построить СДНФ для функции f(x, y, z) = 01111110

6. Построить СКНФ для функции f(x, y, z) = 01101011

7. Построить СДНФ для функции f(x, y, z) = 01110110

8. Построить СКНФ для функции f(x, y, z) = 10100110

9. Построить СДНФ для функции f(x, y, z) = 11110010

10. Построить СКНФ для функции f(x, y, z) = 11100000

Полином Жегалкина

Сложение по модулю два (двоичное сложение) – это новое высказывание, обозначаемое , ложное тогда и только тогда когда, оба высказывания имеют одинаковые логические значения. Приведем таблицу истинности:

x	y
0	0	0
0	1	1
1	0	1
1	1	0

Свойства операции :

1.Операция коммутативна:

2. Операция ассоциативна:

3. Операция дистрибутивна по отношению к операции :

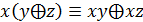
4.Операция не идемпотентна: x .

Полиномом (многочленом) Жегалкина от n переменных называется функция

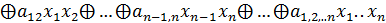
Имеется два способа нахождения полинома Жегалкина. Один из них основан на равносильных преобразованиях для логических функций, заданных в виде ДНФ. Здесь используется факт x . если функция задана в виде ДНФ, то сначала уберем дизъюнкцию, используя при этом законы де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно одному такому слагаемому.

Другой способ основан на построении таблицы истинности для функции. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы значений переменных, начиная с младшего набора и из полученного уравнения находим неизвестный коэффициент. Так как число наборов равно числу коэффициентов, то все коэффициенты определяются однозначно. Для функции от трех переменных полином Жегалкина имеет вид: