Определение предиката. Кванторы

Предикатом P (x ₁, x ₂,..., x_n) называется функция, аргументы которой определены на некотором множестве М, x ₁, x ₂,..., x_n M, а сама она принимает два значения: И (истина) и Л (ложь). Таким образом, предикат осуществляет отображение М {1, 0}.

Переменные x ₁, x ₂,..., x_n называются предметными переменными, а множество M – предметной областью.

Если все переменные x ₁, x ₂,..., x_n принимают конкретные значения, то предикат есть не что иное, как высказывание, Таким образом, высказывание является частным случаем предиката. Можно сказать, что предикат есть высказывание, зависящее от параметров.

Пример.

а) P (x) = «x – четное число». Здесь М – множество целых чисел, xM.

б) A (x, y, z) = «x, y, z лежат на одной окружности». Здесь М – множество точек плоскости, x, y, z M

в) B (x, y) = «x старше y». Здесь M – множество людей, x, y M.

Предикат от n переменных называется n-местным предикатом. Высказывание есть 0-местный предикат.

Как видно из примера, одноместный предикат отражает свойство некоторого объекта, а многоместный предикат выражает отношение между многими объектами.

Над предикатами можно производить обычные логические операции и получать при этом другие предикаты. Таким образом можно говорить об алгебре предикатов.

Пример. Пусть A (x) – предикат «x делится на 3», а B (x) – предикат «x делится на 2». Тогда A (x) Ú B (x) – предикат “ x делится на 3 или на 2”, а A (x) & B (x) – предикат «x делится на 3 и на 2».

Кроме операций логики высказываний, в логике предикатов используются особые логические символы – кванторы (были введены немецким математиком Г. Фреге).

Квантор общности. Пусть P (x) – некоторый предикат, определенный для каждого x Î М. Тогда выражение " xP (x) является истинным высказыванием, если P (x) истинно для всякого x Î М и ложным в противном случае. Символ " x называется квантором общности. Выражение " xP (x) читается: «Для всех x имеет место P (x)». В обычной речи квантору общности соответствуют слова: все, всякий, каждый, любой. Возможно отрицание квантора общности: 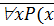): «Не для всех x имеет место P (x)».

Пример. Пусть P (x) – предикат «x – четное число». Тогда " xP (x) есть высказывание «Всякое x – четное число» = «Все числа – четные», которое истинно на множестве M четных чисел и ложно, если М содержит хотя бы одно нечетное число, например, если M – множество целых чисел. Отрицание 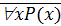есть высказывание «Не всякое x – четное число» = «Не все числа – четные», которое истинно на множестве целых чисел и ложно на множестве четных чисел.

Квантор существования. Пусть P (x) – некоторый предикат, x Î М. Тогда выражение $ xP (x) является истинным высказыванием, если P (x) истинно хотя бы для одного x Î М и ложным в противном случае. Символ $ x называется квантором существования. Выражение $ xP (x) читается: «Существует x, для которого имеет место P (x)». В обычной речи квантору существования соответствуют слова: некоторый, несколько. Возможно отрицание квантора существования: 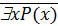: «Не существует x, для которого имеет место P (x)».

Кванторы существования и общности называются двойственными кванторами.

Пример. Пусть, как и в предыдущем примере, P (x) – предикат «x – четное число». Тогда $ xP (x) есть высказывание «Некоторые x – четные числа» = «Существуют четные числа», которое истинно на множестве M, содержащем хотя бы одно четное число и ложно, если М содержит только нечетные числа. Высказывание 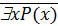= «Неверно, что некоторые x – четные числа» = «Не существует четных чисел» истинно на множестве M, содержащем только нечетные числа и ложно, если М содержит хотя бы одно четное число.

Буква x, стоящая справа от квантора, называется кванторной переменной и должна присутствовать обязательно. Переменная, стоящая под знаком квантора, называется также связанной переменной. Несвязанная переменная называется свободной. Выражения " xP (x) и $ xP (x) не зависят от x и имеют вполне определенные значения. Поэтому переименование связанной переменной, т. е. переход, например, от выражения " xP (x) к " yP (y) не меняет его истинностного значения.

Кванторы могут применяться и к многоместным предикатам. При этом число свободных переменных уменьшается на единицу. Одноместный предикат при связывании переменной квантором становится 0-местным предикатом, т. е. высказыванием.

Не нашли, что искали? Воспользуйтесь поиском: