
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Формулы логики предикатов. Равносильность формул
Формула логики предикатов определяется индуктивно следующим образом:
1. Любая формула логики высказываний есть формула логики предикатов.
К новым формулам логики предикатов относятся следующие выражения:
2. Если x, y, z,... – предметные переменные, то предикаты P (x), Q (x, y),..., а также выражения с кванторами " xP (x), $ xR (x), " x $ yQ (x, y),... есть формулы.
3. Если A и B – формулы, то 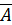 , A Ú B, A
, A Ú B, A  B, A
B, A  B, A ~ B есть формулы, в которых свободные переменные формул A и B остаются свободными, а связанные переменные формул A и B остаются связанными.
B, A ~ B есть формулы, в которых свободные переменные формул A и B остаются свободными, а связанные переменные формул A и B остаются связанными.
4. Ничто, кроме указанного в пунктах 1 – 3, не есть формула.
Пусть A – формула, содержащая свободную переменную x. Тогда " xA, $ xA – формулы, причем в первом случае A является областью действия квантора общности, а во втором – областью действия квантора существования.
Пример.
1. Следующие выражения являются формулами логики предикатов:
а) A  B C, где A, B, C – высказывания.
B C, где A, B, C – высказывания.
б) " x $ yQ (x, y, z)  " x $ yP (x, y, u).
" x $ yP (x, y, u).
Проанализируем последовательно это выражение.
Предикат Q (x, y, z) – формула;
Выражение " x $ yQ (x, y, z) – формула; переменные x, y – связанные, переменная z – свободная.
Предикат P (x, y, u) – формула.
Выражение " x $ yP (x, y, u) – формула; переменные x, y – связанные, переменная u – свободная.
Выражение " x $ yQ (x, y, z)  " x $ yP (x, y, u) – формула; переменные x, y – связанные, переменные z, u – свободные.
" x $ yP (x, y, u) – формула; переменные x, y – связанные, переменные z, u – свободные.
2. Выражение " x $ yP (x, y, z)  Q (x, y, z) формулой не является. Действительно, выражение " x $ yP (x, y, z) есть формула, в которой переменные x и y связанные, а переменная z свободная. Выражение Q (x, y, z) также формула, но в ней все переменные x, y, z свободные.
Q (x, y, z) формулой не является. Действительно, выражение " x $ yP (x, y, z) есть формула, в которой переменные x и y связанные, а переменная z свободная. Выражение Q (x, y, z) также формула, но в ней все переменные x, y, z свободные.
Формулы F и G, определенные на некотором множестве М, называются равносильными на этом множестве, если при любых подстановках констант вместо переменных они принимают одинаковые значения.
Формулы, равносильные на любых множествах, будем называть просто равносильными.
Переход от одних формул к равносильным им другим формулам логики предикатов может быть произведен по следующим правилам:
1. Все равносильности, имеющие место для логики высказываний, переносятся на логику предикатов.
2. Перенос квантора через отрицание.
Пусть A – формула, содержащая свободную переменную x. Тогда
 º $ x
º $ x 
 º " x (
º " x ( ).
).
Правило переноса квантора через знак отрицания можно сформулировать так: знак отрицания можно ввести под знак квантора, заменив квантор на двойственный.
Справедливость равносильностей вытекает из смысла кванторов. Так, левая часть может быть прочитана следующим образом: «Неверно, что для всякого x имеет место A (x)». В правой же части утверждается: «Существует x, для которого A (x) не имеет места». Очевидно, что оба утверждения одинаковы. В левой и правой частях соответственно содержатся одинаковые утверждения: «Неверно, что существует x, для которого имеет место A (x)» и «Для всех x не имеет места A (х)».
Пользуясь равносильностями, а также равносильностями логики высказываний, можно для каждой формулы найти такую равносильную ей формулу, в которой знаки отрицания относятся к элементарным высказываниям и элементарным предикатам.
Пример.
 º
º  º " x (
º " x ( )) º " x (A (x)
)) º " x (A (x) 
 )) º " x (A (x)
)) º " x (A (x)  $ y
$ y 
3. Вынос квантора за скобки.
Пусть формула A (x) содержит переменную x, а формула B не содержит переменной x, и все переменные, связанные в одной формуле, связаны в другой. Тогда
" x A (x)Ú B º " x (A (x)Ú B).
" x A (x)  B º" x (A (x)
B º" x (A (x)  B).
B).
$ x A (x)Ú B º $ x (A (x)Ú B).
$ x A (x)  B º $ x (A (x)
B º $ x (A (x)  B).
B).
4. Дистрибутивность квантора общности относительно конъюнкции и квантора существования относительно дизъюнкции.
Пусть формула B, так же, как и формула A, зависит от х. Тогда
" xA (x)  " xB (x) º " x (A (x)
" xB (x) º " x (A (x)  B (x)).
B (x)).
$ xA (x) Ú $ xB (x) º $ x (A (x)Ú B (x)).
Дистрибутивные законы для квантора общности относительно дизъюнкции и квантора существования относительно конъюнкции, вообще говоря, не имеют места, т. е. формулы " xA (x)Ú" xB (x) и " x (A (x)Ú B (x)), а также $ xA (x)  $ xB (x) и $ x (A (x)
$ xB (x) и $ x (A (x)  B (x)) не являются равносильными, хотя они могут быть равносильными на некоторых множествах М.
B (x)) не являются равносильными, хотя они могут быть равносильными на некоторых множествах М.
Пример. Показать, что формулы " x (A (x) Ú B (x)) и " xA (x) Ú " xB (x)) не равносильны.
Пусть М – множество натуральных чисел, A (х) = «х – четное число», B (х) = «х – нечетное число». Тогда
" x (A (x) Ú B (x)) = «Всякое натуральное число четное или нечетное» = 1.
" xA (x) = «Всякое натуральное число – четное» = 0,
" xB (x) = «Всякое натуральное число – нечетное» = 0,
" xA (x) Ú " xB (x) = «Всякое натуральное число четное или всякое натуральное число нечетное» = 0, т. е. формулы " x (A (x) Ú B (x)) и " xA (x) Ú " xB (x) не равносильны.
5. Перестановка одноименных кванторов.
" x " yA (x, y) º " y " xA (x, y).
$ x $ yA (x, y) º $ y $ xA (x, y).
Разноименные кванторы переставлять, вообще говоря, нельзя.
Пример. Пусть М – множество натуральных чисел, A (x, y) = «x > y».
" x " yA (x, y) = «Для всех x и y имеет место x > y» = Л;
" y " xA (x, y) = «Для всех у и х имеет место х > y» = Л;
" x " yA (x, y) º " y " xA (x, y).
6. Переименование связанных переменных.
Заменяя связанную переменную формулы A другой переменной, не входящей в эту формулу, всюду: в кванторе и в области действия квантора, получим формулу, равносильную A.
Пример.
A = " xF (x)  $ xG (x).
$ xG (x).
Заменяя связанную переменную x на y в первом члене импликации и на z во втором, получим равносильную формулу:
B = " yF (y)  $ zG (z).
$ zG (z).
A º B.
Задания:
1. Используя аксиомы, формулы и правила вывода исчисления высказываний, вывести формулу (АÚВ) → (ВÚА)
2. Используя аксиомы, формулы и правила вывода исчисления высказываний, вывести формулу (
3. Построить вывод формул: 
4. Построить вывод формул: 
5. Построить вывод формул: 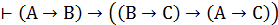
6. Построить вывод формул: 
7. Построить вывод формул: 
8. Построить вывод формул: 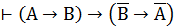
9. Изобразите на координатной плоскости области истинности предикатов:

10. Изобразите на координатной плоскости области истинности предикатов:

11. Изобразите на координатной плоскости области истинности предикатов:

12. Изобразите на координатной плоскости области истинности предикатов:

13. Найдите область истинности и область определения предиката:

14. Найдите область истинности и область определения предиката:

15. Найдите область истинности и область определения предиката:
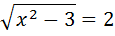
16. Найдите область истинности и область определения предиката:

17. Даны предикаты  :
:  и
и  :
:  , определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны:
, определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны:
1)  2)
2) 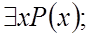 3)
3)  4)
4)  .
.
18. Пусть даны предикаты: P (x): «x – четное число» и Q (x): «x кратно 3», определенные на множестве N. Найти области истинности предикатов:
1)  2)
2)  3)
3)  4)
4)  .
.
Не нашли, что искали? Воспользуйтесь поиском: