
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Высказывания, операции над высказываниями
Высказывание – это повествовательное предложение, относительно которого имеет смысл утверждать, что оно является истинным либо ложным. Таким образом, отличительной особенностью высказываний является возможность принимать одно из двух значений: истина – 1, ложь – 0. Эти значения называются истинностными значениями.
Например, высказывание «Москва — столица Российской Федерации» является истинным, а высказывание «Волга впадает в Черное море» — ложным.
Задание: укажите, какие из высказываний являются истинными и какие — ложными.
а) 3+2 = 5; б) 3< 2; в) 3х < 2; г) у2 ≤ 0;
д) «Число слов в этом предложении равно семи»;
е) «Осень — лучшая пора года»;
ж) «Знаете ли вы украинскую ночь?»;
з) «В четырехугольнике противоположные стороны конгруэнтны»;
и) «Во всяком четырехугольнике противоположные стороны конгруэнтны»;
к) «В некоторых четырехугольниках противоположные стороны конгруэнтны»;
л) «Существует число х такое, что х2 < 0»;
м) «Для всякого числа х |х| > 0»;
н) «В городе N более 100 000 жителей»;
о) «Существует наибольшее натуральное число»;
п) H20+S03=H2S04.
Высказывания бывают:
1. Простыми – если в них нельзя выделить часть, которая сама является высказыванием и не совпадает по смыслу с исходными;
2. Составными – в противном случае.
Простые высказывания будем обозначать малыми буквами латинского алфавита, а факт истинности или ложности высказывания записывать собственно: а = 1 или а = 0.
Буквы, обозначающие переменные высказывания, будем называть высказывательными переменными.
Для конструирования составных высказываний из простых используют так называемые логические связки:
1. не; неверно, что;
2. и; а; но;
3. или; либо;
4. если, то;
5. тогда и только тогда, когда.
Логические операции над высказываниями:
1. Отрицанием высказывания а называется новое высказывание, обозначаемое  и читаемое не а, неверно, что а, которое является истинным тогда и только тогда, когда высказывание а ложно, и наоборот.
и читаемое не а, неверно, что а, которое является истинным тогда и только тогда, когда высказывание а ложно, и наоборот.
2. Конъюнкцией двух высказываний а и b называется новое высказывание, обозначаемое  , которое истинно тогда и только тогда, когда оба высказывания истинны и ложное во всех остальных случаях.
, которое истинно тогда и только тогда, когда оба высказывания истинны и ложное во всех остальных случаях.
3. Дизъюнкцией двух высказываний а и b называется высказывание, обозначаемое  , которое является ложным тогда и только тогда, когда ложны оба высказывания и истинное во всех остальных случаях.
, которое является ложным тогда и только тогда, когда ложны оба высказывания и истинное во всех остальных случаях.
4. Импликацией двух высказываний а и b называется высказывание, обозначаемое  , которое является ложным тогда и только тогда, когда 1-ое высказывание а истинно, а второе высказывание b – ложно.
, которое является ложным тогда и только тогда, когда 1-ое высказывание а истинно, а второе высказывание b – ложно.
5. Эквиваленцией двух высказываний а и b называется высказывание, обозначаемое  , которое является истинным тогда и только тогда, когда оба высказывания принимают одинаковые значения истинности.
, которое является истинным тогда и только тогда, когда оба высказывания принимают одинаковые значения истинности.
Под формулой в логике высказываний будем понимать:
- любое конкретное или любое переменное высказывание
- если а и b формулы, то формулами также являются

- других формул, кроме указанных выше, нет
Под таблицей истинности будем понимать перечень всех логических возможностей формулы с указанием значений истинности самой формулы в каждой логической возможности.
| a | b | 
| 
| 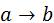
| 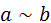
|
Запишем определения логических операций в виде таблицы истинности:
| а | 
|
Формула называется выполнимой, если она принимает значение «истинна», хотя бы в одной своей логической возможности и не является тавтологией.
Для любых формул A, B, C справедливы следующие равносильности:
1. Коммутативность.
а) A  B º B
B º B  A (для конъюнкции);
A (для конъюнкции);
б) A Ú B º B Ú A (для дизъюнкции).
2. Ассоциативность.
а) A  (B
(B  C) º (A
C) º (A  C)
C)  C (для конъюнкции);
C (для конъюнкции);
б) A Ú (B Ú C) º (A Ú B) Ú C (для дизъюнкции).
3. Дистрибутивность.
а) A  (B Ú C) º A
(B Ú C) º A  B Ú A
B Ú A  C (для конъюнкции относительно дизъюнкции);
C (для конъюнкции относительно дизъюнкции);
б) A Ú(B  C) º (A Ú B)
C) º (A Ú B)  (A Ú C) (для дизъюнкции относительно конъюнкции).
(A Ú C) (для дизъюнкции относительно конъюнкции).
4. Закон де Моргана.
а) 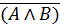 º
º 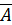 Ú
Ú  (отрицание конъюнкции – дизъюнкция отрицаний);
(отрицание конъюнкции – дизъюнкция отрицаний);
б) 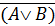 º
º 
 (отрицание дизъюнкции – конъюнкция отрицаний).
(отрицание дизъюнкции – конъюнкция отрицаний).
5. Идемпотентность.
а) A  A º A (для конъюнкции);
A º A (для конъюнкции);
б) A Ú A º A (для дизъюнкции).
6. Поглощение.
а) A  (A Ú B) º A (1– ый закон поглощения);
(A Ú B) º A (1– ый закон поглощения);
б) A Ú A  B º A (2– ой закон поглощения).
B º A (2– ой закон поглощения).
7. Расщепление (склеивание).
а) A  B Ú A
B Ú A  (
( ) º A (1–ый закон расщепления);
) º A (1–ый закон расщепления);
б) (A Ú B)  (A Ú
(A Ú 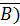 º A (2–ой закон расщепления).
º A (2–ой закон расщепления).
8. Двойное отрицание.
 º A.
º A.
9. Свойства констант.
а) A  1 º A; б) A
1 º A; б) A  0 º 0; в) A Ú1 º 1; г) A Ú 0 º A; д)
0 º 0; в) A Ú1 º 1; г) A Ú 0 º A; д)  º 1; е)
º 1; е)  º 0.
º 0.
10. Закон противоречия.
A 
 º 0.
º 0.
11. Закон “исключенного третьего”.
A Ú 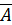 º 1.
º 1.
12. A  B º
B º 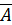 Ú B.
Ú B.
13. A ~ B º (A  B)
B)  (B
(B  A) º (A
A) º (A  B) Ú (
B) Ú (
 .
.
Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа «º».
Пример:


1. Составить таблицу истинности для формулы 
2. Составить таблицу истинности для формулы 
3. Составить таблицу истинности для формулы 
4. Составить таблицу истинности для формулы 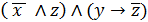
5. Составить таблицу истинности для формулы

6. Составить таблицу истинности для формулы 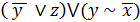
7. Доказать равносильность  .
.
8. Доказать равносильность  .
.
9. Используя таблицу истинности доказать равносильность
(x → y) → (x ∧ y ~ (x  y)) = (x ∧ y → x)→ y.
y)) = (x ∧ y → x)→ y.
10. Упростить формулу  .
.
Постройте таблицу истинности формулы:
11.1. (A ∨В)→(С →B);
11.2. (А∧В)∨(С→А);
11.3. (А∨В)≡  ;
;
11.4. ((А≡В)∧С)→(С∧А);
11.5. ( ∧В)→С;
∧В)→С;
11.6.  )≡(
)≡( ∨
∨  );
);
11.7. (С→(А∨В))∧((В∧С)→А);
11.8. ( ∨В)∧(В∨С);
∨В)∧(В∨С);
11.9. (А∨В)→ 
11.10. (А→(С∨В))∧((А∧С)→В);
11.11. (А∨В)→( →(В∧А)).
→(В∧А)).
Нормальные формы
В алгебре высказываний используют две нормальные формы: дизъюнктивную и конъюнктивную нормальные формы формулы (ДНФ и КНФ).
ДНФ формулы есть формула, равносильная исходной формуле логики высказываний и записанная в виде дизъюнкции элементарных конъюнкций переменных, т.е. F = K 1Ú K 2Ú K 3Ú..., где Ki = A  B
B  C
C  ....
....
КНФ формулы есть формула, равносильная исходной формуле логики высказываний и записанная в виде конъюнкции элементарных дизъюнкций переменных, т.е. F = D 1  D 2
D 2  D 3
D 3  ..., где Di = A Ú B Ú C Ú....
..., где Di = A Ú B Ú C Ú....
Наибольшее распространение в логике высказываний получили формулы вида КНФ, элементарные дизъюнкции которых Di принято называть дизъюнктами, а члены каждого дизъюнкта A, B, C – атомами.
Пример. Указать, в каких нормальных формах находятся следующие формулы логики высказываний.
a) A – ДНФ и КНФ
b) (A Ú B)  C – КНФ
C – КНФ
c) A Ú  Ú
Ú  – ДНФ и КНФ
– ДНФ и КНФ
d) (A Ú B)  (
( Ú C) – КНФ
Ú C) – КНФ
e) A Ú B  C – ДНФ
C – ДНФ
f) A 

 – ДНФ и КНФ
– ДНФ и КНФ
g) A  B Ú
B Ú  C – ДНФ
C – ДНФ
Для каждой формулы логики высказываний функции F имеется равносильная ей дизъюнктивная нормальная форма (ДНФ) и конъюнктивная нормальная форма (КНФ).
Алгоритм приведения формул логики высказываний к ДНФ (КНФ).
Шаг 1. Все подформулы F вида A 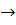 B (т.е. содержащие импликацию) заменяем на
B (т.е. содержащие импликацию) заменяем на  Ú B или на
Ú B или на  .
.
Шаг 2. Все подформулы F вида A ~ B заменяем на (A  B) Ú (
B) Ú ( ) или на (A Ú
) или на (A Ú  )
)  (
( Ú B).
Ú B).
Шаг 3. Все отрицания, стоящие над сложными подформулами, опускаем по законам де Моргана.
Шаг 4. Устраняем все двойные отрицания над формулами.
Шаг 5. Осуществляем раскрытие всех скобок по закону дистрибутивности конъюнкции относительно дизъюнкции для ДНФ или по закону дистрибутивности дизъюнкции относительно конъюнкции для КНФ.
Пример. Дана формула F = A  B
B  (A Ú B). Привести формулу к виду ДНФ:
(A Ú B). Привести формулу к виду ДНФ:
1) F = ( Ú
Ú  )
)  (A Ú B);
(A Ú B);
2) F = ( A) Ú (
A) Ú ( B) Ú (
B) Ú ( A) Ú (
A) Ú ( B);
B);
3) F = ( B) Ú (
B) Ú ( A).
A).
Если каждая элементарная конъюнкция (или элементарная дизъюнкция) формулы содержат символы всех переменных, то такая формула называется совершенной. Есть совершенные дизъюнктивные нормальные формы формулы (СДНФ) и совершенные конъюнктивные нормальные формы формулы (СКНФ).
«Свойства совершенства»:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в запись формулы.
2. Все логические слагаемые различны.
3. Ни одно логическое слагаемое не содержит одновременно переменную и ее отрицание.
4. Ни одно логическое слагаемое не содержит одну и ту же переменную дважды.
Не нашли, что искали? Воспользуйтесь поиском: