Основные законы теории множеств.

1. Коммутативность операций ∪ и ∩:

A ∪ B = B ∪ A A ∩ B = B ∩ A

2. Ассоциативность операций ∪ и ∩:

A ∪(B ∪ C)=(A ∪ B)∪ C A ∩(B ∩ C)=(A ∩ B) ∩ C

3. Законы идемпотентности операций ∪ и ∩:

A ∪ A = A A ∩ A = A

4. Законы дистрибутивности:

A ∪(B ∩ C)=(A ∪ B)∩(A ∪С) A ∩(B ∪ C)=(A ∩ B) ∪ (A ∩С)

5. Законы поглощения:

A ∪(A ∩ B)= A A ∩(A ∪ B)= A

6. Законы де Моргана:

= ∩ = ∪

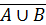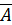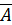7. Законы пустого и универсального множеств:

A ∪∅= A A ∩∅= ∅ A ∩ A =∅

A ∪ U = U A ∩ U = A A ∪ A = U

=∅ = U

8. Закон двойного отрицания:

= A

Задача 1

Заданно универсальное множество и четыре его подмножества , , 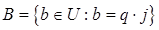, где i,j,k,n=1,2,…

p=5, q=3, r=10, s=9.

Решение

Из условия следует, что множества A,B,C,D состоят из следующих элементов.

A={5,10,15,20,25,30,35,40,45,50,55,60} все числа кратные 5 от 1 до 60.

B={3, 6, 9, 12, 15,18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60} все числа кратные 3 от 1 до 60.

C={10, 20, 30, 40, 50, 60} все числа кратные 10 от 1 до 60.

D={9, 18, 27, 36, 45, 54} все числа кратные 9 от 1 до 60.

Объединение множеств

По сути это те и только те элементы которые не делятся ни на 5, ни на 3.

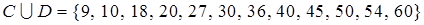
Пересение двух множеств

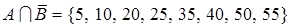
Ответ: во множестве 32 элемента.

1. Заданы множества A ={1,2,3,4,5,6} B ={3,4,5,6,7,8}.Найти объединение, пересечение, разности этих множеств

2. Определить результаты операций , если

3. Пусть А – множество натуральных чисел, кратных 2; В – множество натуральных чисел кратных 3. Найти АÈВ, АÇВ, А\В, В\А.

4. Пусть А – множество различных букв слова «множество»; В – множество различных букв слова «содружество». Найти АÈВ, АÇВ, А\В, В\А.

5. Пусть А – множество различных букв слова «МАТЕМАТИКА», В – множество различных букв слова «ЛОГИКА». Найти АÈВ, АÇВ, А\В, В\А.

6. Пусть А = { (x, y) | x<y}; В = {(x, y) | y >0 } Изобразить множества АÇ В, В А, А\ В, В\А.

7. Даны множества A = {1,5,7,137}, B = {5,7,23}, C = {0,1,5, 23}, D = {0,7,23,1998}. Найдите множество (A B) \ (C D)

Доказать тождества, используя определения операций над множествами:

8.

9.

10.

11.

12.

13.

14.

15.

16.

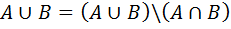
17.

Не нашли, что искали? Воспользуйтесь поиском: