Основные операции над множествами

Название операции	Пересечение множеств	Объединение множеств	Разность множеств	Дополнение к множеству А	Симметрическая разность
Обозначение			А \ В
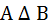
Изображение кругами Эйлера
Определение	Те и только те элементы, которые принадлежат одновременно А и В	Те и только те элементы, которые принадлежат хотя бы одному из множеств А и В	Те и только те элементы множества А, которые не принадлежат В	Те и только те элементы, которые не принадлежат множеству А (т.е. дополняют его до универсального U)	Те и только те элементы, которые принадлежат одному из множеств: А либо В, но не являются общими элементами
Символическая запись				=

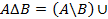
Рассмотрим пример. Пусть А = {а, b, с, g, е}, В = {а, с, e, f, r, т}, тогда А В = {а, b, с, g, e, f, r, т), А В = {а, с, е}, A\B = {b, g}, В\А = {f, r, m}, A B={b, g, f, r, т}. Обратим внимание, что для разности двух множеств не выполняется переместительный закон: А\В В\А. Это становится очевидным, если одно множество пустое (например, A), а другое — непустое.

Способы задания множества:

1) Множество может быть задано с помощью перечисления (указания) всех его элементов, заключенных в фигурные скобки. Например, запись A ={1,5} задает множество A, которое состоит из двух элементов – чисел 1 и 5.

2) Множество может быть задано с помощью характеристического свойства его элементов. Например, множество A, состоящее из элементов x, являющихся четными числами, можно записать следующим образом:

A ={ x | x – четное число}. В такой записи слева от вертикальной черты задается природа элемента (единичный элемент, пара элементов, множество, цепочка символов и т.п.), а справа – характеристическое свойство.

Введем обозначения для наиболее часто используемых множеств:

N – множество всех натуральных чисел;

Z – множество всех целых чисел;

Z+ – множество целых неотрицательных чисел (Z+ = N ∪{0});

Z– – множество целых неположительных чисел (Z– = Z \ N);

Q – множество всех рациональных чисел;

R – множество всех действительных чисел;

R+ – множество неотрицательных действительных чисел;

R– – множество неположительных действительных чисел.

Не нашли, что искали? Воспользуйтесь поиском: