Скаляр аргументті векторлық функция.

а)І деп сандық аралықты (сандық сигментті [ а,в ], сандық (а,в) интервалды, [ а,в), (а,в ] сандық жартылай интервалды, сандық түзуде R-ді) белгілейік. Үш өлшемді евклидтік кеңістік Е₃ -те үш өлшемді V₃ векторлық кеңістікті қарастырайық.

Сандық І жиынын әрбір t санына үш өлшемді V₃ кеңістіктегі векторын сәйкестендіретін заң не ереже берілсе, онда І сандық аралықта t скаляр аргументті вектор-фнукция берілді дейді. Оны деп жазады.

Бұл вектор-функцияның модулі сандық мәндер қабылдайтын кәдімгі функция болады.

І аралықта анықталған функция нүкте аймағында шексіз кіші делінеді, егерде бұл аймақта шексіз, шексіз кіші шама болса, яғни болса.

вектор функцияның нүктедегі шегі деп айырым шексіз кіші болатын тұрақты векторын айтады және оны былайша етіп жазады.

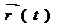Егер бұл шек -ның нүктедегі мәніне тең болса, яғни болса, онда вектор функция нүктеде үздіксіз функция делінеді. Ал, І аралықтағы барлық нүктесіндегі үздіксіз болса, онда ол І аралықта үздіксіз деп аталады.

Егер -ға болатындай өсімше берілсе, вектор-функция 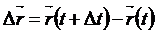өсімше алады. Сонда мына шек бар болса, онда нүктеде дифференциалданатын вектор функция делінеді.

Оны былайша немесе қысқаша деп жазады.

Сонымен

Мұны вектор функция -ның гі туындысы дейді. (ал -ны t нүктедедгі дифференциалы дейді). І аралықтың әр нүктесінде туындысы болса, онда функция І аралықта дифференциалданатын вектор –функция делінеді.

б) функция І аралықта берілсін. Е₃ евклидтік кеңістікке ортонормаланған 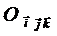координата жүйесін ендірейік. вектор базистік векторларға былайша жіктелсін.

(57-1)

Онда сол І аралықта анықталған үш скаляр (сан) функция оның координаталары болады. Олар t-ның нақты бір мәнінде сандар болады.

(57-1)-ден вектор функция нүктеде үздіксіз болу үшін сандық функциялардың сол нүктеде үздіксіз болуының қажеттілігі мен жеткіліктігі шығады.

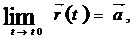Егер тұрақты вектор болса, онда болтындықтан болу үшін болудың керектігі шығады.

Теорема. І аралықта координаталары арқылы берілген векторлық функция нүктеде дифференциалданатын функция болу үшін функциялар сол нүктеде дифференциалданатын функциялар болулары керек.

Бұл кезде (57-2) болады.

Дәлелі t-ға t өсімше берсек функция өсімше алар еді; Бұдан . Бұдан жоғарыда айтқанымыздай шек болу үшін , ,

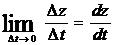
Шектеудің болуы керектігі шығады. Демек (57-2) дұрыс.

в) Векторлық функциялар үшін мына формулалар дұрыс болады.

(скаляр көбейтінді)

(векторлық көбейтінді)

скаляр функция)

шынында да ортонормаланған базисте болса, онда болатындықтан (57-2) бойынша.

басқаларында осылай дәлелдейді.

Лемма. Егер 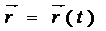вектор І аралықта бағыты өзгеріп ұзындығы өзгермейтін вектор болса (мысалы бірлік вектор болса онда вектор І аралықтың әр нүктесіндегі өзінің туындысына ортогонал болады.

Шынында да болса болады да, бұдан туындыға көшсек Ал, бұл 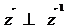деген сөз.

Егер 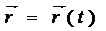вектор бағыты өзгермейтін ұзындығы өзгеретін вектор болса, онда ( -бірлік вектор болады.

Бұдан туынды алсақ 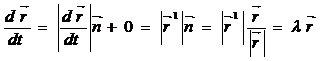сонымен ал бұл ¹пен өзара коллиниар болады деген сөз.

Сонымен бағыты өзгеріп ұзындығы өзгермейтін вектор функция өзінің туындысына перпендикуляр, ал бағыты өзгермей ұзындығы өзгеретін вектор-функция өзінің туындысы мен коллиниар болады екен.

Ескерту І аралықта анықталған функцияның туындысында сол аралықта анықталған функция болатындықтан оны тағы да дифференциалдауға болады.

Оларды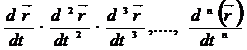

деп белгілейді. Немесе деп жазатын боламыз.

Сызық ұғымы

а) Элементар сызықтар. Евклидтік Е₃ кеңістікте ортонармаланған репер берілсін М кеңістік нүктесі болса, онда ол нүктені радиюс векторы делінеді. Егер м нүкте кеңістікте қозғалысқа енсе оның t моменттегі орнын 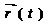вектор функция анықтар еді. Сөйтіп t уақыт І аралықта өзгергенде осы І аралықта анықталған вектор функция жасалады. Оның t моменттегі координаталары х(t), у(t), z(t) болса 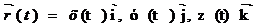(57-4) болар еді.

Мұны М нүктенің қозғалыс заңы дейді (362-сурет)

z М

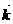
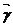
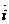у

0 362-сурет

t аргумент І аралықта өзгергенде М нүкте кеңістікте қандайда бір траектория Г жасайды. Сөйтіп функция t -ның өзгеру арлығы І мен М нүкте траекториясы Г арасында өзара сәйкестік орнатады. Егер бұл сәйкестік өзара бір мәнді және үздіксіз бейнелеу болса, яғни І мен Г арасында гомеоморфизм орнатса, онда нүктелер траекториясы Г элементар қисық (немесе элементар сызық)

делінеді.

Евклидтік кеңістікте түзуді, сәулені, кесіндіні қарапайым сызық (қарапайым қисық) дейді.

Қарапайым сызықтардың біріне гомeоморфты болатын фигураларды элементар сызық (қисық) дейді. Оның ішінде кесіндіге гомеморфты элементар сызық доға делінеді.

Егер l түзуіне координата жүйесін ендірсе, онда әрбір санға координаты осы болатын М нүктесін сәйкестендіруге болады. Бұл сәйкестік гомеоморфизм болады. Сондықтан бұлайша бейнелеуде сандық түзуі түзуіне, сандық интервалы, координаталары А В болатын ұшы жоқ АВ кесіндіге (ол түзуге гомеоморфты болады) ал сандық сигмент ұшы бар АВ кесіндіге, ал сандық интервал В ұшы жоқ Ав кесіндіге гомеоморфты болады. Сөйтіп сандық аралықтың кез-келгені қарапайым сызықтың біріне гомеоморфты болады екен. Сондықтан қандайда бір сандық аралыққа гомеоморфты болатын фигураны элементар қисық деуге де болады.

Ұшы бар жарты шеңбер ұшы бар кесіндіге, үшы жоқ жарты шеңбер түзуге гомеоморфты болатыны айтылған. Демек жарты шеңбер элементар сызық болады.

Синусойда, косинусойдалар абсцисса өсіне гомеоморфты болатындықтан оларды элементар сызық болады.

Сөйтіп Евклид кеңістігіне тікбұрышты координаталар жүйесін ендірce элементар сызықтар мынадай

x=(x(t), y=y(t), z=z(t) (57-5)

теңдеулер жүйесімен анықталады екен. Мұндағы t қандай да бір І аралықта өзгереді, ал x(t), y(t), z(t) ол аралықта үздіксіз функциялар. Бұл теңдеуді элементар сызықтық параметрлік теңдеуі дейді.

Жалпы І аралықта үздіксіз x(t), y(t), z(t) үш функция элементар сызықты анықтау үшін оның бірі бұл аралықта қатаң үдемелі функция болуы керек.

б) сызық (қисық) жалпы қисық немесе сызық деп шекті немесе санаулы элементар сызықтармен жабуға болатын фигураны айтады. Мысалы 363-суреттегі (шеңберді АТВ,СNК доғалармен (доға элементар сызық) жазуға болады. Гипербола, тангенсойда, катангенсойдалар сызық болады.

T

C N

A B

K

363-сурет

L Сызығының М нүктесі оның жай (кәдімгі) нүктесі делінеді, егерде М -ның u(М,ε) аймағы табылып онымен L -дің қимасы (яғни L u(М,ε) фигура) элементар сызық болса кері жағдайда айрықша нүктесі делінеді. Мысалы 334-а суреттегі L сызығы үшін М жай N айрықша нүкте. Егер

L u(М,ε) қима

а) б) в) г)

түзуге гомеоморфты болса М ішкі нүкте сәулеге гомеоморфты болса шекаралық нүкте (не сызықтың ұшы) делінеді.

Әрбір нүктесі жай (кәдімгі) нүкте болатын сызықты жай сызық дейді. Демек элементар сызықтар жай сызық болады. Шеңбер, эплипс. Жай сызық болады, бірақ олар элементар сызық болмайды. Өйткені олар қарапайым сызықтардың ешқайсысымен гомеоморфты емес.

Паскаль Улиткасы (364-б сурет). Кардиоида (364- в сурет), Бернулли Лемнискоты (364-2 сурет) жай сызық болмайды. Өйткені оларда бір-бірден айрықша нүкте бар. Олар 0 нүктесі

в) жатық сызық. Г₀ элементар сызық , , 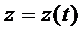параметрлік теңдеумен берілсін, t қандай да бір І аралықта өзгерсін.

Г₀ элементар сызығы С^к-класын жатық (тегіс, жылтыр) сызық делінеді. Егерде функциялардың І аралықта к -ға дейінгі ретті үздіксіз туындылары болса (к натурал сан) және І-дың әрбір t нүктеде оларды t арқылы алынған туындылардың жасалған матрица ронгы 1-ге тең болса

Ранг (x¹(t) y¹(t) z¹(t))=1 (57-6)

Бұл t- ның ешбір мәнінде х¹, у¹,z¹ туындалар қатарынан 0-ге болатын деген сөз.

Мысалы, синусойда теңдеуін кеңістікте параметр арқылы былайша x=t, y=sint, z=0, t k жазуға болады. Бұл функциялардың бүкіл R-де кез-келген ретті үздіксіз туындаылары бар және x¹=1 y¹=cos t z¹=0 болғандықтан (57-6) орындалады. Демек синусойда с^∞ классты жатық сызық болады.

Г жай сызық C^k (k ≥ 1) классты жатық сызық делінеді, егерде оның әрбір ішкі нүктеісі м -нің U(м, ε ) aймағы болып, онымен Г сызықтық қимасы

Г U(м, ε ) с^к- классты жатық (элементар) сызық болатын болса.

Шеңбер с^∞ классты жатық сызық болады.
Өйткені шеңбердің жазықтағы x=r cos t, y=r sint теңдеуін O 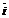координата жүйесінде x=r cos t, y=rsint, z=0 деп жазуға болады. Ал, мұның бүкіл R сандық түзуде ∞ дейінгі туындысы бар және болатындықтан (57-6) шарты орындалады.

г) үздікті – жазық сызық параметрлік x=x(t), y=y(t), z=z(t) (57-6) теңдеуімен Г жай сызық берілсін, t қандайда бір u олысты өзгерсін. Ол сызық үздікті – жатық сызық делінеді. Егерде u облыста қайсының ішінде (57-5) теңдеу жатық – сызықты анықтайтын санаулы I_k бөлік жиындарымен жазуға болатын болса (бұл бөлік араласатын ұштарында жатық болмауы да мүмкін).

Мысалы 365-суретте x= a (t-sint), y= a(1-cost), z=0 теңдеуімен берілген циклы кескінделген. Ол түзуге гомомрфты, оған оны О_Х өсіне ортоганал роекциялау арқылы көз жетізуге болады.

у

х

Сондықтан циклоид элементар сызық болады x=2akπ, k=±1, ±2… нүктелерде x¹=0, y¹=0, z¹=0 болғндықтан (156-6) шaрт орыдалмайды. Сондықтан ол жатық сызық болмайды. Циклоид теңдеуі бүкіл R – түзуде анықталған. Сондықтан R түзуді I_k= [ 2a (k-1) π, 2akπ ] кесінділермен жазуға болады. Ол кесінділер ішінде циклонд үздікті – жатық сызықты анықтайды. Демек циклоид үзікті – жатық сызық болады.

Е₃ евклидтік кеңістікке тікбұрышты координалар жүйесі ендірілсе түзуді (бұл жатық сызықтық дербес түрі болады) (57-7) екі тәуелсіз теңдеулер жүйесімен беруге болады.

Бұл теңдеулер жүйесі жатық сызықты анықтау үшін: 1-ден , функциялар үздіксіз және үздіксіз туындылары болулары куерек.

Егерде ≠0 болса, онда сызық теңдеуін (57-9) түрде жазуға болады. Бұл теңдеуді параметрлік формада былайша жазуға болады.

х=t, y=y(t), z=z(t) (57-9-a)

O_xyz координатa жүйесінде жатық сызық (157-5) теңдеумен берілген болды. Оларды сәйкесінше 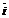базистік векторларға көбейтіп қоссақ, ол 3 скаляр функцияға эквивалентті болатын бір векторлы функция

(57-10) шығады

Сонда (56-8) жарты t-ның ешқандай мәнінде болу керек дегенді білдіреді.

(57-10) Сызықтың векторлық теңдеуі делінеді, ол (57-9,а) формуламен берлген үш скаляр теңдеуімен эквиввлиентті болады.

Не нашли, что искали? Воспользуйтесь поиском: