Гомеоморфты кеңістікке мысалдар.

1- мысал. Топологиясын метрика ρ индукциялаған эквлидтік Е₃ және табиғи топологиясы R³ сандық кеңістіктерді қарастырайық.

Егер Е₃ –ке О_хуғ тік бұрышты координаталар жүйесін ендірсек Е₃-тен әрбір M нүктесіне R³ тің f(M) = m = (x₁, x₂, x₃ сaны (координаталары) сәйкес келетіндіктен, олар арасында f: E₃→R³ бейнелеу арнайды және ол өзара бірмәнді бейнелеу болады. Сонымен қатар f: E₃→R³ үздіксіз бейнелеу болады. Өйткені M_o E₃ нүктенің R³ –дегі бейнесі f(M_o)=m_o=(x₀₁,x₀₂, x₀₃) дейік, R³ –тен m₀ нүктенің аймағы W_o -ды алайықта m₀ нүктені қамтитын

W_o -ге енетін W (a_i<x_oi < b_i ашық координаттық паралелпипедті қарастырайық.

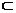Егер E үшін | a_i-x_oi |, | b_i-x_oi | i=1,2,3 сандардың ең кішісін алсақ, онда М₀ -дың аймағы и үшін f(u) W 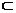W₀ болар еді. Демек f бейнелеу М₀ нүктеде үздіксіз ал М₀ нүкте Е₃ –тің кезкелегн нүктесі болғандықтан f үздіксіз бейнелеу болады.

Үздіксіз бейнелеуге кері бейнелеуде үздіксіз бейнелеу болатындықтан f: E₃→R³ гомеомороризм болады, яғни E₃ ~ R³ болады.

Осы сияқты E₂ ~ R², E₁ ~ R¹, A₃ ~ R³, A₂ ~ R² , A ~ R¹ болатындығын дәлелдеуге болады.

2- мысал. Екі өлшемді Е₂ эвклидтік кеңістікте ұштарын А,В нүктелері, центірі О болатын жарты шеңбер γ берілген, АВ диаметріне паралель d жанама түзу жүргізілген. А,В нүктелердің d - дағы артогонал проекциялары А₀,В₀ нүктелер болсын (330-сурет) А₀,В₀ =I кесінді дейік.

Е₂ кеңістіктің топологиясы ол жазықтықтан (Е₂ кеңістіктегі) γ жиында (шеңберде) Ф топология, I = А₀,В₀ кесіндіде Г топология индукциялайды.

(γ,ф), (I, r) топологиялық кеңістіктер болады. Осы кеңістіктердің гомеоморфты болатынын дәлелдеу керек.

Дәлелі f: γ → d бейнелеуді γ жарты шеңберді d түзуге ортогонал проекциялау болсын. Онда ол өзара бір мәнді бейнелеу болатыны түсінікті. Енді оның үздіксіз бейнелеу болатынына көз жеткізейік. Ол үшін γ дан бір нүкте алайық, оның d -дағы ортогонал проекциялаудағы бейнесі N_o=f(N) болсын N_o кез келген V аймағы үшін N нүктенің f (u) 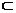V болатын u аймағын көрсетуге болады.

A 0 B

N

C

A_o C_o N_o B_o d

V

330-сурет.

Сондықтан f бейнелеу N нүктеде үздіксіз болады. Ал, N нүкте γ шеңбердің еркін алынғандықтан f бүкіл γ -да үздіксіз болады. Сондықтан оған кері f¹ демек f – гомеомороризм сөйтіп ұштары бар (жоқ) жарты шеңбер ұштары бар (жоқ) кесінді мен гомеоморфты болады екен.

Егер φ бейнелеуі ұштары жоқ жарты шеңбер γ -ны шеңбер центірі О нүктесіне d түзуіне o d=C_o заңмен орындалатын центірлік проекциялау болса, онда ол φ: γ¹ → d бейнелеу гомеоморфизм болады:

Екі f^-1 : I¹→ γ¹, φ: γ → d гомеоморфизмнің көбейтіндісі φ f ¹ -де гомеоморфизм болады. Демек ұшы жоқ I¹=(Ao Bo) кесінді түзуге гомеоморфты болады екен. Бұдан (а_хв) сандық интервал R сандық түзуге гомеоморфты болатынын шығады.

Осы әдіспен мына тұжырымдардың дұрыстығын дәлелдеуге болады.

1. Жиегі бар (жоқ) жарты сфера тұйық (ашық) дөңгелекке гомеоморфты болады.

2. Ашық дөңгелек жазықтыққа гомеоморфты болады.

3. Дөңес көпбұрыш тұйық дөңгелекке гомеоморфты болады.

4. Сәуле [ a b) жарты нинтервалға гомеоморфты болады.

Мысалы 331суретте α жазықтығында К дөңгелек берілген. Оған жарты сфера салынған. Сфераға α – ға параллель β жанама жазықтығы жүргізілген.

β

y α

γ →

331-сурет

К ның шекарсы γ шеңбер. К -ның Х нүктесіне сфераның ортогонал проекцияны х болатын у нүктесі сәйкестендірілген Oy β=Z болсын. Бұл у- тегі О центрлі проекция. Сонда x k нүктені сәйкестендіретін бейнелеу гомеоморфизм болады. Демек ашық дөңгелек жазықтыққа гомеоморфты болады. Осы сияқты жиегі бар (жоқ)жарты сфера тұйық (ашық) дөңгелекке гомеоморфты болады.

Не нашли, что искали? Воспользуйтесь поиском: