
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исықтың қисықтығы мен бұралуы.
Қисықтың қаншалықты бұралынқылығын (қисайғанның, майысқанның) анықтау жалпы түрде қисықтың қисықтығын (яғни түзу сызықтан қаншалықты ауытқығанның) сипаттау үшін қисық бойындағы нүктенің қозғалуына сай қисықтың әр нүктесінен жүргізілген жанамаларының бағыттарының өзгеру жылдамдығын анықтауу (салыстыру) керек. Бұл өзгеру жылдамдық қай жерде көп болса, сол қисайған деуге яғни қисықтығы көп деуге болады. Түзудің кез келген нүктесінен жанама сол жүргізілген жанама сол түзудің өзімен беттеседі. Сондықтан түзудің нүктелерінен жүргізілген жанамаларының бағытының өзгеру жылдамдығы 0 болады. Демек түзу қисаймаған, қисықтығы 0 болатын фигура болады.
L жатық сызық, ρ мен Θ оның бойында жақын жатқан нүктелер болсын. Ол нүктелерден 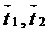 бағытты жанамалар жүргізсек, олар арасындағы бұрыш θ, ал θ ρ -доға Δs болса, онда
бағытты жанамалар жүргізсек, олар арасындағы бұрыш θ, ал θ ρ -доға Δs болса, онда  қатынас жанам бағытының өзгеру жылдамдығын сипаттар еді, оны Θ ρ доғаның орташа қисықтығы дейді (38-а сурет)
қатынас жанам бағытының өзгеру жылдамдығын сипаттар еді, оны Θ ρ доғаның орташа қисықтығы дейді (38-а сурет)
Ал θ → ρ ұмтылғандағы ол орташа қисықтықтың шегін 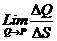 қисықтың ρ нүктедегі қисықтығы дейді. Оны К десек
қисықтың ρ нүктедегі қисықтығы дейді. Оны К десек 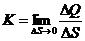 . Ол жанаманың өзгеру жылдамдығын сипаттайды.
. Ол жанаманың өзгеру жылдамдығын сипаттайды.





 ∆ θ t(s)
∆ θ t(s) 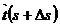 A
A

 ρ Θ С
ρ Θ С
a O B
ρ В)
а) б)
368-сурет
Теорема. Ск классты жатық L сызықтың өзінің әбір нүктесінде қандайда бір қисықтығы К болады және L сызық табиғи параметрмен
 =
=  (s)=x(s)
(s)=x(s) 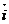 + y(s)
+ y(s) 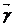 + z(s)
+ z(s)  (58-13) болып берілсе ол қисықтық мынаған тең болады.
(58-13) болып берілсе ол қисықтық мынаған тең болады.
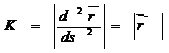 (58-14)
(58-14)
Дәлелі ρ, θ нүктелерге параметрдің S, S+ΔS мәндері сай келсін (368-б сурет). Ол нүктеден жүргізілген жанамалардың бірлік векторлары 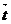 (s),
(s), 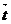 (s+Δs) болсын және олар арасындағы бұрышты θ дейік
(s+Δs) болсын және олар арасындағы бұрышты θ дейік 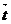 (s) жанама болғандықтан
(s) жанама болғандықтан 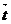 (s) =
(s) =  және шарт бойынша
және шарт бойынша 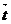 (s) бірлік вектор. Демек
(s) бірлік вектор. Демек 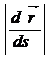 =1
=1
O нүктеден  векторларды өлшеп салайық (368-в сурет). Сонда
векторларды өлшеп салайық (368-в сурет). Сонда 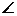 AOB= θ болады және
AOB= θ болады және 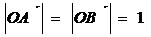 .
.
Сондықтан ос биссектриса болса 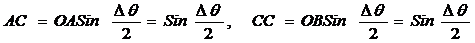 болатындықтан AB=2Sin
болатындықтан AB=2Sin 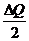 болады.
болады.
Сонда 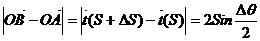 болады да
болады да 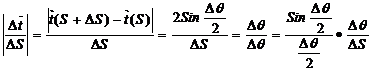 болады.
болады.
Ал, ΔS → 0 ұмтылғанда Δ θ → 0 ұмтылатынын ескерсек және соңғы теңдікте жекке көшсек 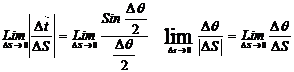
Сонымен 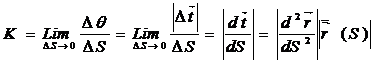 болып, теорема дәлелденеді. Сөйтіп k>0 және S -тың функциясы болады екен. k=k(s)
болып, теорема дәлелденеді. Сөйтіп k>0 және S -тың функциясы болады екен. k=k(s)
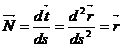 векторды L қисықтың ρ нүктедегі қиысқытың векторы, ал оның ұзындығын
векторды L қисықтың ρ нүктедегі қиысқытың векторы, ал оның ұзындығын 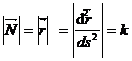 қисықтың сол нүктедегі қисықтығы дейді, оның кері шамасын
қисықтың сол нүктедегі қисықтығы дейді, оның кері шамасын  қисықтың ρ нүктесі қисықтғының радиусы дейді. Сонымен қисық табиғи парметрмен
қисықтың ρ нүктесі қисықтғының радиусы дейді. Сонымен қисық табиғи парметрмен 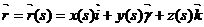 теңдеумен берілген онда ол қисықтың қисықтығы мына формуламен табылады екен.
теңдеумен берілген онда ол қисықтың қисықтығы мына формуламен табылады екен.
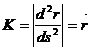 (58-14a)
(58-14a) 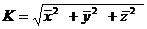 (58-14б)
(58-14б)
Мұндағы 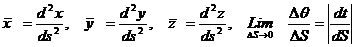 теңдіктен оның сол жағы
теңдіктен оның сол жағы 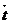 бірлік вектордың бұрыштық жылдамдығын білдіретіндіктен бірлік вектордың бұрыштық жылдамдығы 1-туындысының модуліне тең болатындығы шығады.
бірлік вектордың бұрыштық жылдамдығын білдіретіндіктен бірлік вектордың бұрыштық жылдамдығы 1-туындысының модуліне тең болатындығы шығады.
Қисықтың М нүктесінен қисықтық векторы 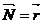 векторға паралель бағытта жүргізілген векторды түзуді сол L қисықтық М нүктедегі бас нормалы дейді, ал
векторға паралель бағытта жүргізілген векторды түзуді сол L қисықтық М нүктедегі бас нормалы дейді, ал 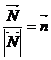 вектор бас нормалдық бірлік векторы делінеді.
вектор бас нормалдық бірлік векторы делінеді.
Сонда 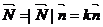 . Сөйтіп
. Сөйтіп  немесе
немесе 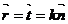 (58-15) бірлік вектор өзінің бірінші туындысына перпендикуляр болады деген лемма бойынша
(58-15) бірлік вектор өзінің бірінші туындысына перпендикуляр болады деген лемма бойынша 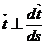 немесе
немесе 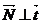 . Сөйтіп бас нормал
. Сөйтіп бас нормал  жанама вектор
жанама вектор 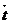 ға перпендикуляр болады екен. Сондықтан
ға перпендикуляр болады екен. Сондықтан 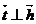 болады.
болады.
Жанаманың бірлік векторы 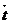 мен бас нормалдың бірлік векторы
мен бас нормалдың бірлік векторы 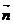 -нің векторлық көбейтіндісін
-нің векторлық көбейтіндісін  дейік
дейік
 =
= 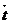

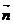 (58-16)
(58-16)
М нүктеден  векторға паралель етіп жүргізілген (M,
векторға паралель етіп жүргізілген (M,  ) түзу L сызықтың М нүктедегі бинормалы делінеді. Векторлық көбейту анықтамасы бойынша
) түзу L сызықтың М нүктедегі бинормалы делінеді. Векторлық көбейту анықтамасы бойынша 
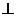
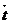 ,
, 
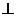
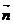 болады және
болады және 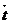 мен
мен 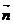 арасындағы бұрышы 900 болғандықтан және |
арасындағы бұрышы 900 болғандықтан және |  |=|
|=| 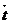 ||
|| 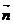 | sin(
| sin(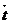 ^
^ 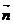 )=1
)=1  1
1  1=1 болатындықтан
1=1 болатындықтан  вектор бірлік вектор болады, оны бинормалдың бірлік векторы дейді.
вектор бірлік вектор болады, оны бинормалдың бірлік векторы дейді.
Сонымен жатық сызықтың кезкелген М нүктесінен өзара перпендикуляр үш түзу өтеді екен.
Олар: Жанама түзу, оның білрік векторын 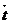 дейік, бас нормал түзуі,
дейік, бас нормал түзуі, 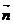 дедік бинормал түзуі
дедік бинормал түзуі  дедік.
дедік.
Сондықтан бұлар ортанормаланған Rm=(M 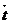
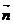
 ) репер анықтайды. Оны L қисықтың канондық репері дейді.
) репер анықтайды. Оны L қисықтың канондық репері дейді.
Бұлар қос-қостан өзара перпендикуляр үш жазықтықты анықтайды. Оны Френе үшжағы дейді. Бұлар канондық репердің координаттық жақтары болады.
Оларды былайша атайды:
- М нүкткесі жанама түзу, бас нормал арқылы өтетін (M 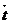
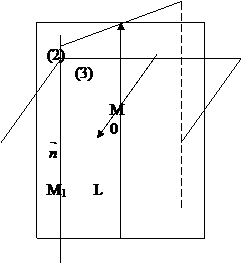
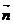 ) жазықтықты L -дің жанасу жазықтығы дейді, оған бинормал перпендикуляр болады (369-суретте 1 жазықтық)
) жазықтықты L -дің жанасу жазықтығы дейді, оған бинормал перпендикуляр болады (369-суретте 1 жазықтық)
- М нүктесі бас нормал, бинормал арқылы өтетін (M 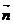
 ) жазықтықты нормал жазақтық дейді, оған жанама түзу перпендекуляр болады (369-суретте 2 жазықтық)
) жазықтықты нормал жазақтық дейді, оған жанама түзу перпендекуляр болады (369-суретте 2 жазықтық)
- М нүктесі, жанама түзу мен бинормал түзу арқылы өтетін (M 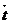
 ) жазықтықты түзуленетін жазықтық делінеді, оған бас нормал перпендекуляр болады (369-суретте 3 жазықтық)
) жазықтықты түзуленетін жазықтық делінеді, оған бас нормал перпендекуляр болады (369-суретте 3 жазықтық)
Бұл суретте ММ1 -жанама түзу ММ2 бас нормал түзуі ММ3 бинормал түзуі 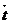 - бірлік вектор жанама бойымен параметрдің көбею жағына қарай бағытталады.
- бірлік вектор жанама бойымен параметрдің көбею жағына қарай бағытталады.
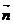 - бас нормалдың бірлік векторы қисықтың ойыс жағына қарай
- бас нормалдың бірлік векторы қисықтың ойыс жағына қарай
M3
 (1)
(1)
 M2
M2
 | |||
 |
369-сурет
бағтталады. 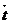 бинормал
бинормал 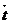 ,
, 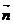 ,
,  векторлар осы орналасуында оң үштік 369-сурет жасайтындай болып бағытталады.
векторлар осы орналасуында оң үштік 369-сурет жасайтындай болып бағытталады.
Не нашли, что искали? Воспользуйтесь поиском: