Есеп. Евклидтік жазықтықта мына жиындар

а) Жазықтықтың әрқайсысының кемінде бір рационал координаты бар нүктелерінің жиыны.

б) жазықтықтың тек бір рационал координаты бар нүктелерінің жиыны.

в) Жазықтықтың дәл екі рационал координатты бар нүктелерінің жиыны.

Байламды жиын болады ма, болмайды ма?

Шешімі:

Топологиялық (Т,Ф) кеңістік байламды делінеді егер оны (Т -ны) өзара қиылыспайты некі ашық жиынның біріктірмесі түрінде өрнектеуге болмайтын болса.

Х жиыны топологиялық Т кеңістікте байламды делінеді. Егерде ол Т -да байламды ішкі (бөлік) кеңістік болса, басқаша х жиыны топологиялық Т кеңістікте болса байламды делінеді, егерде х жиынынан мынадай болатын екі ашық u,v жиын табылмаса.

(u x) ( v x)= x, (u x) ( v x)= , u x=

Басқаша х жиыны Т топологиялық кеңістікте байламды делінеді, егер оны мынадай болатын u v = u v = u және v жиындардың бріктімесі түрінде өрнектеуге болмаса.

Топологиялқ Т кеңістік байламды емес делінеді, eгерде u v = , u v =t болатын екі ашық u,v жиын табылса.

Бұл кезде u, v жиын бірін – бірі Т – ға толықтырушы жиындар болады.

C_Tu=V C_T V=u бұдан Т байламды жиын делінеді; егерде онда бірденнен әрі ашық, әрі тұйық болатын Т жиын немес бос жиын ғана болатын болса деген тұжырымшығады.

а) жағдай жазықтықтағы ең болмағанда бір координаты рационал болатын нүктелер жиыны Т дейік. Бұл жиындағы бір координаты рационал сан болатын нүктелер жиынтығы А₁ екі координаты рационал сан болатын нүктелер жиынын В₁ десек, онда А₁ 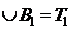болады, A₁ B₁ не бірінші не екінші координаты рационал сан болатын нүктелер жиынынан тұратындықтан ол бос емес жиын болады. Сонымен А₁ 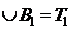, A₁ B₁ ≠ болды. Демек Т₁ жиын байламды жиын болады.

б) Жағдай. жазқтықтағы тек бір координтты рационал сан болатын нүктелер жиынын Т₂ дейік. Бірінші координаты х ₁ екінші координаты у рационал сан болатын нүктелер жиынын А₂, В₂ дейік. Сонда A₃ B₃ =T₂ болатыны түсінікті, ал А₂ В₂= бос жиын болады. Сонымен A₂ B₂ =T₂, А₂ В₂= демек Т₂ байламды емес жиын.

в) Жағдай π жазықтықтың екі координатыда рационал сан болатын нүктелерінің жиынын Т₃ дейік. Мұның ішінде1-координаты x< болатын нүктелер жиынын Т₃, болатын нүктелер жиынын B₃десек A₃ B₃=T₃ болады, ал A₃ B₃ бірінші координаты болатын нүктелер жиыны болар еді, бұл рационал емес, иррационал сан, сондықтан Т₃ -ке ол кірмейді. Сондықтан A₃ B₃ бос жиын болады. Сөйтіп A₃ B₃=T₃ A₃ B₃= демек Т₃ жиыны байламды емес жиын болады.

8- есеп. Евклидтік Е₃ кеңістікте мына жиындар:

а) Ашық жарты жазықтық,

б) Бүкіл жазықтық

в) болатын x²+y²+z²≤a² а≠0 болатын M(x, y, z) нүктелер жиыны

г) Ортақ нүктесі жоқ екі ашық дөңгелек нүктелерінің жиыны. Облыс боладыма, жоқпа?

Шешуі: Облыс деп кезкелген байламды ашық жиынды айтады. Сондықтан ашық жарты жазықтық бүкіл жазықтық облыс болады, ал x²+y²+z²≤a² нүктелер жиыны тұйық шар болатындықтан облыс болмайды (ашық емес), ал ортақ нүктесі жоқ екі ашық дөңгелек байланысты жиын емес айырылған жиын болғандықтан облыс болмайды.

9- есеп. Евклидтік Е₃ кеңістіктің төмендегі жиындары компакты болады ма, жоқпа?

а) Нүктелердің ақырлы жиыны

б) Ашық дөңгелек, яғни OM<r болатын M нүктелердің жиыны

в) Тордың бетімен ішкі нүктелерімен тұратын жиыны.

г) Координаталары 1, шексіз жиын құрайтын О_х осінің нүктелерінің жиыны.

Шешуі: (Т,Ф) топологиялық кеңістіктің ашық Т₂ кейбір ішкі жиындарының жинағы ашық жабу делінеді, егер 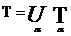(біріктірмесі) болса.

Топологиялық Т кеңістік компакты (немесе компак) делінеді. Егер оның әрбір ашық жабуында ақылы ішкі жабу болса.

Евклидтік кеңістіктің ішкі жиыны компакты болу үшін ол тұйық және шектелген болуы керек.

Осыны ескерсек

а) Нүктелердің ақырлы жиыны шектелген және тұйық болғандықтан компакты жиын болады.

б) Ашық дөңгелек шектелген, бірақ тұйық болғандықтан (шектелген болсада) компакты жиын болмайды.

в) Тордың ішкі және шекаралық нүктелерінің жиыны компакты болады. Өйткені ол жиын тұйық және шектелген.

г) Нүктелер жиыны шектелген (1-ден көп емес, 0-ден аз емес) бірақ тұйық емес сондықтан компакты жиын болмайды.

10- есеп. Тұйық дөңгелек, тұйық сақина. Крендель екі тесікті, n бұрышты пирамиданың Эйлер характеристикасын табыңдар.

Шешуі: Егер көпбейнелік клеткаларға жүктелген болса және ол клеткаларының төбелерінің саны _o, қабырғасының соны ₁ клетканың саны ₂ болса, онда _{= 1}- ₂+ ₃ санын,ол көпбейнеліктердің Эйлер характеристикасы дейді.

а) Сонда тұйық дөңгелек үшбұрышқа гомеоморфизм болатындықтан, үшбұрышта _o=3 төбе, ₁= 3 қабырге және ₂=1 клетка болатындықтан тұйық дөңгелектің Эйлер характеристикасы (тұйық дөңгелек) = _o- ₁ + ₂=3-3+1=1 ге тең болады.

б) Тұйық сақина 2 тесікті сфераға гомеоморфты болады. Сфераның Эйлер характеристикасы (тэтраэдрге гомеоморфты болатындықтан және тэтраэдрде _o= 4 төбе, ₁=6 қабырға ₂=4 клетка (жоқ) болатындықтан) (сфера) = 4-6+4=2 ге тең болады. Егер сферада к тесік болса, оның Эйлер характеристикасы =2-k.

в) Крендель 4 тесікті сақинаға гомеоморфты, сондықтан оның Эйлер характеристикасын =2-4=-2 болады.

г) π бұрышты пирамида _o=n+1 төбе, ₁=2n қабырға (қaр) ₂=n+1 жоқ болады. Сондықтан оның Эйлер характеристикасы = n+1-2n+n+1=2 болады.

Не нашли, что искали? Воспользуйтесь поиском: