Метрикалық және топологиялық кеңістіктер. Гомеоморфизм.

Топология эленменттері

51.1 Метрикалық кеңістік. М жиынның кез келген реттелген х, у екі элементіне оң нақты ρ(x,y) саны төмендегі 3 шарт орындалатындай етіп сәйкестендірілсін: М-1 х=у болғанда, тек сонда ғана ρ (х,у)=0 болсын, М-2 кез келген x,y элементтер үшін ρ (х,у)= ρ (у, х) болсын,

M-3 x,y,z элементтер үшін ρ (х,у)+ ρ (y, z)= ρ (х,z) болсын, онда М жиынында метрика ρ анықталған делінеді.

М жиынын бұл жиында анықалған ρ метрикасы ρ мен, қоса яғни (М, ρ) жұбын метрикалық кеңістік дейді. М жинының элементтерін ол кеңістіктің нүктелері М – 1,2,3 шарттарды ол кеңістіктің аксиомалары ρ (х,у) санын кеңістіктің х, у нүктелерінің арақашықтығы дейді.

Егер R⁺ деп оң нақты сандар жиынын белгілесек, М жиынындағы ρ (х,у) метриканы М – 1,2,3 аксиомаларды қанағаттандыратын ρ: М x М→ R⁺

Бейнелеу ретінде қарастыруға да болады.

Евклидтік Е₃ кеңістікке метриканы ρ(А,В)= (51-1), Сандық кесінді [a,b] - ға ρ (х,у)=|y-x | формулалармен ендіруге болады. Өйткені бұл формулалар М– 1,2,3 аксиомаларды қанағаттандырады.

Оң нақты r > 0 санын және (М, ρ) метрикалық кеңістіктің х₀ нүктесін алайық. Онда бұл кеңістіктің мына талаптарды

ρ (х₀,x)< r, ρ (х₀,x) ≤ r, ρ (х₀,x)= r (51.3)

Қанағаттандыратын х нүктелерінің жиынын сәйкесінше, центірі х₀ радиyсы r болатын ашық шар, тұйық шар, сфера дейді.

Радиусы ε центірі х₀ болатын W(x₀, ε) ашық шарды х₀ нүктесін. ε - аймағы дейді.

(М, ρ) метрикалық кеңстіктегі N ішкі жиыны болсын. М -нің, х нүктесінің N жиынында толығымен жататын ең болмағанда бір аймағы болса, ол N -нің ішкі нүктесі, N -нің нүктелері кірмейтін аймағы болса N -нің сыртқы нүктесі, a N -нің де N -ді М -ге толықтыратын М\N жиынында (мұнда қысқаша С_п N деп белгілейді) нүктелері кіретін аймағы болса N -ші шекаралық нүктесі делінеді.

N жиынының барлық ішкі нүктелерінің мен жиынын ол жиынның іші дейді. Оның int N (int француздың интер бер деген сөзі) немесе N деп белгілейді. Барлық сыртқы нүктелерінің жиынын N деп белгілейді, барлық сыртқы нүктелерінің жиынын ext N(ext – француздың экстерь деген сөз) деп белгілейді. Барлық шекаралық нүктелердің жиынын шекара дейді, оны Ғ _r N (Ғ _r - frontien деген сөз) деп белгілейді.

Кез келген М жиыны үшін мына қатыс орындалатыны түсінікті

int М F_rM ext М = М, int M FrM ext= .

N жиынын шектелген делінеді, егер ол толығымен жататын шар табылса, табылмаса шектелмеген делінеді. Мысалы кесінді, элипс шектелген, түзу гипербола шектелмеген жиын.

Тек ішкі нүктелерден тұратын жиын ашық жиын делінеді.

Метрикалық кеңістікте кезкелген ашық жиындардың біріктірілмесі де, қимасы да ашық жиын болады.

Метрикалық кеңістіктің барлық ашық жиындарының жиынынына (жүйесіне) сол кеңістіктің өзі де, бос жиында кіреді.

51.2 Топологиялық кеңістік. Т жиынынан әйтеуір бір жол мен оның оның ішкі жиындары Т₂ -лер жүйесі Ф={T₂} бөліп алынсын және ол төмендегі 3 талапты қанағаттандырсын.

Т-1 T жиынының өзі мен бос жиын Ф – ға кіретін болсын,

Т-2 Ф жиындар жүйесінің кез келген жиындарының біріктірілмесі Ф -қа кіретін болсын,

Т-3 Ф жиындар жүйесінің кез келген жиындарының қимасы Ф -ға кіретін болсын.

Онда Т жиынында Ф={T₂} топологиялық құрылым немесе қысқаша Ф={T₂} топология анықталған делінеді, және Т жиынды онда анықталған топологиясымен қоса, яғни (Т,Ф) жұбын топологиялық кеңістік дейді.

Т- ның элементтерін ол кеңістіктің нүктелері, топология Ф -ның элементтерін топологиялық кеңістіктен ашық жиындары, ал Т-1,2,3 талаптарды Ф топологияның (топологиялық кеңістіктің) аксиомалары дейді.

Топологиялық кеңістікке мысалдар.

1- мысал. Кез келген Т жиын берілсін. Оның ішкі ашық жиындары жүйесі үшін сол жиынның өзі Т мен бос жиынды алайық, яғни Ф={T, } екі элементтерінен тұрсын бұл жағдайда Ф үшін Т – 1,2,3 талаптың үшеуіде орындалады.

Шынында да Т-1 орындалады,себебі Ф осы Т мен құралған.

T =T, T = болатындықтан -ның элементтерінің біріктірілмесі де, сөйтіп φ={T} T-1.2.3 аксиоманың үшеуінде қанағаттандырады Қимасы да Ф -ға кіреді. Сондықтан Ф={T φ} жиын Т жиын үшін топологиялық құрылым болады. Сондықтан анықтама бойынша (Т, Ф) жұбы топологиялық кеңістік болады. Оны антидискретті (немесе триволды) топологиялық кеңістік дейді.

2- мысал. Тағы да сол Т жиыны берілсін, бұл жиындағы ашық жиындар жүйесі үшін Т -ның барлық ішкі жиындарының жиынын (үйірін) алайық. Сонда Ф жүйе Т-1,2,3 аксиоманың үшеуінде қанағаттандырады. Сондықтан Ф топология (Т,Ф) – топологиялық кеңістік болады Ф-ны бұл кезде дискритті топология (Т, Ф) ны дискритті топологиялық кеңістік дейді.

Бұл екі мысалдан бір жиынға әртүрлі топология ендіру арқылы (яғни Т -дағы ашық жиындар үшін әртүрлі жиындарды алу арқылы) әртүрлі топологиялық кеңістік шығарып алуға болатыны көрінеді.

3- мысал. (М,ρ) метрикалық кеңістік болсын. Мұндағы ашық жиындар үйірі Ф үшін бұл кеңістікті ашық шарлар жиыны алынсын.

Метрикалық кеңістікке 51.1 –де айтылғандай М жиынын өзіде, бос жиында енетіндіктен және ашық жиындардың біріктірмесі де тумасы да енетіндіктен (М,ρ) метрикалық кеңістік топологиялық кеңістік болады. Оның топологиясы ашық шарлар жүйесінен тұрады. Бұл топология митрика ρ арқылы индукциялнған делінеді.

4- мысал. Rⁿ=R x R x … x R (n рет) жиыны берілсін. R нақты сандар жиындар. Сонда Rⁿ деген (x₁, x₂, …, x_n) түрдегі n сандар тобынан тұратын сандар жиыны. Бұл Rⁿ жиынына ашық жиындар ұғымын ендірейік. (a_i, b_i), i=1,2,…,n түрдегі n сандық интервал алайық. Мынадай a_i<x_i<b_i, i=1,2,…,n болатын M (x₁, x₂, …, x_n) нүктелер жиынын координаттық паралипипед дейді.

Rⁿ –нің W жиынын ондаған ашық жиын дейміз, егер ол өзінің әрбір нүктесімен қатар, ол нүкте енетін қандайда бір ашық координаттық паралипипедтіде қамтитын болса осылайша Rⁿ -де анықталған ашық жиындар үйірі Т-1,2,3 аксиомаларды қанағаттандырады. Сондықтан W жиынр жүйесі Ф берілген Rⁿ жиында анықталған топология болады. Оны табиғи топология дейді. Ол топология Rⁿ -ді топологиялық кеңістікке айналдырады. Оны сандық сандық кеңістік дейді, n=1 болғанда ол түзу болады.

5- мысал. Аффиндік, проективтік кеңістіктер топологиялық кеңістік болады.

Мысалы П₂ -аффиндік жазықтық, АВСД=W ондағы параллелогрм болсын. Сонда

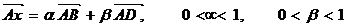
Теңдігін қанағаттандыратын х нүктелер жиынын АВСД параллелограмның ішкі нүктелер жиыны int W -ны береді. П₂ -ші ішкі жиыны ашық жиын делінеді, егер ол өзінің әрбір нүктесімен ол нүкте енетін қандай да бір ашық паралелограмның ішінде қамтитын болса. П₂ -де осылайша анықталған ашық жиындар жүйесі Ф Т-1,2,3 аксиомаларды қанағаттандырады. Сондықтан ол П₂ жазықтық үшін топология болады, aл (П₂,Ф) топологиялық кеңістік болады. Осы сияқты n -өлшемді аффиндік А_п кеңістікте топологиялық топологиялық кеңістік болатынына көз жеткізуге болпады.

Не нашли, что искали? Воспользуйтесь поиском: