Топологиялық кеңістіктің базасы.

Топологиялық (Т,Ф) кеңістіктің ашық жиындарының үйірі В кеңістік топологиясы Ф -ның базасы делінеді, егерде Т -ның әрбір нүктесі х және оның кезкелген U _х аймағы үшін В -да x B_x 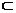U _х болатын В_х элемент бар болса кезкелген топологияның әйтеуір бір базасы болады. Мысалы Ф -ның өзін база ретінде алуға болады;

Евклидтік кеңістегі ашық шарлар жиыны, оның топологиялық базасы болады; Нақты сандар жиыны R интервалдар жиыны оның табиғи топологиясының базасы болады; Rⁿ жиындағы ашық координаттық паралелпипедтер жиынын сандық Rⁿ кеңіс тіктің табиғи топологиясы үшін база болады.

Топология базасының негізгі қасиеті мына теоремада берілген.

Теорема. Топологиялық (Т,Ф) кеңістіктің ашық ішкі жиындарының үйірі В кеңістік топологиясы Ф -ның әрбір элементі В -ның элементтерінің біріктірмесі болатын жағдайда ғана, тек сол жағдайда ғана Ф топологияның базасы болады;

Дәлелі. (Т,Ф) топологиялық кеңістікттің топологиясы Ф- үшін В оның базасы болсын, U кеңістіксіз кезкелген ашық жиыны болсын, яғни U 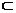Ф болсын. Яғни U 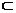Ф болсын. Онда кезкелген x u нүкте үшін базалық анықтамасы бойынша x b_x 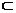u болатын В_х элемент В -да бар болады. В-дағы осындай В_х элементтер жиынын қарастырайық бұл кезде Х, U-дың кез келген элементі болғандықтан, әрине U жиынын В_х элементтердіңен біріктірмесі болады. Бұған кері ұйғарымның дұрыстығы айқын.

Егер (Т,Ф) топологиялық кеңістіктің топологиясы Ф -ның Т жиынын санаулы не ақырғы ішкі ашық жиындағы үйірін тұратын ең болмағанда бір базасы болса, онда (Т,Ф) санаулы базасы топологиялық кеңістік делінеді.

Мысалы. Сандық түзу R санаулы базасы топологиялық кеңістік болады. Өйткені R сандық түзудің табиғи топологиясы рационал ұшты интервалдар үйірінен тұрады бұл база санаулы.

Осы сияқты Rⁿ сандық кеңістікте санаулы базасы кеңістік болады бұлардан аффиндік,евклидтік кеңістіктерден де санаулы базасы кеңістік болатыны шығады.

Топологиялық кеңістікте оның жиынының ішкі, сыртқы, шекаралық нүктелер ұғымы. Жиынның ішкі шекарасы ұғымдары метрикалық кеңістіктегідей анықталады. Мұнда да өзінің ішімен беттесетін жиындар ғана ашық жиын болады.

Топологиялық кеңістіктің х нүктесінің аймағы мен ол кеңістіктің ішкі N жиынының қимасы бос жиын болмаса, онда х нүкте N жиынын жанасу нүктесі делінеді.

Демек, анықтама бойынша жиынның кезкелген нүктесі және кез келген нүктесі шекаралық нүктелер ол жиынға жанасу нүкте болады.

N жиынның барлық жанасу нүктелерінен жиынын (яғни N жиынның ішімен шекаралық нүктелерінің біріктірмесін ол жиынның тұйықталуы дейді, оны 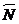деп жазатын боламыз..

Сонда 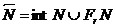(51-5) болады. Мысалы (а,в) сандық интервалдың тұйықталуы [ a, b ] кесінді, ашық дөңгелектің тұйықталуы тұйық дөңгелек болады.

N жиынының сыртқы нүктелері оның тұйықталуына енбейтіндіктен жиынның тұйықталуының толықтырушысы (яғни T \ 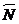=C_T N) сол N жиынының толықтыушысының (яғни int (T \ N)=C_T N) бейнеленеді.

Т \ N =int (Т \ N) немесе C_T 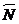=C_T N (51-6)

Топологиялық (Т,Ф) кеңістікте N жиын тұйық делінеді, егерде оның толықтырушысы С_т N ашық жиын болса.

[a, b] кесінді, тұйық дөңгелек, тұйық шар тұйық жиын болады.

Топологиялық кеңістік бірденнен әрі тұйық, әрі ашық болады.

Теорема. Ттопологиялық (Т,Ф) кеңістікте R жиыны өзінің тұйықталуы пен беттескен жағдайда ғана тек сол жағдайда ғана тұйық болады.

Дәлелі. (Т,Ф) кеңістікте х тұйық жиын болсын. Онда оның толықтырушысы С_тХ ашық болғандықтан ол Ф -ға енеді. C_TX 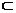Ф.

Ал С_тХ ашық болғандықтан ол өзінің іші мен беттеседі (56-1) бойынша C_tX = C_tX бұл екеуінен C_tX = C_tX бұдан х=x. Енді керісінше х=x болсын С_tХ= С_tХ. бұдан С_tХ ашық жиын болатынн, сондықтан оның топология Ф -ға кіретіні шығады. Бұдан Х -жиыны тұйық жиын болатыны шығады.

Егер Х топологиялық кеңістік (Т,Ф) – ның ішкі жиыны болса және топология Ф -ның элементтері W_o - лер мен Х жиынының қималарының жиынын Г={W_O x} десек, онда (x, r) жұбы да топологиялық кеңістік болады. Өйткені ол Т-1,2,3 аксиомаларды қанағатттандырады (x, r) кеңістікті (Т,Ф) топологиялық кеңістіктен ішкі (бөлік) кеңістігі дейді, оның топологиясы Г -ны Х жиынды Ф топрология индукциялаған дейді.

Мысалы евклидтік Е₂ жазықтықтың топологиясы осы жазықтағы γ шеңбердің тополлогиясы Ф₀ -ды индукциялайды. Бұл топология элементтері Е₂ жазықтықтағы ашық жиындармен γ шеңбердің қималарынан тұрады. Сонда (γ,Ф₀) топологиялық кеңістік болады және ол Е₂ тополгиялық кеңістіктің ішкі кеңістігі болады.

51.4 Гомеоморфизм. (Т₁,Ф₁), (Т₂,Ф₂) екі топологиялық кеңістік берілсін. Т₁-ді Т₂- ге бейнелеу f: T₁→ T₂ x T нүктелерді үздіксіз бейнелеу делінеді, егер оның бейнесі f(x) -тың Т₂ -дегі кезкелеген аймағы U^l үшін, Х -тың Т₁ -де U аймағы табылып f(u) 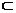u болса.

Егер Т₁-дің әрбір нүктесінде f үздіксіз болса, онда жай ғана үздіксіз бейнелеу дейді.

Теорема. (Т,Ф) топологиялық кеңістікті (Т₂,Ф₂) топологиялық кеңістікке бейнелеу Т₂- дегі кезкелген ашық жиынның Т₁ -дегі түп бейнесі де ашық жиын болғанда ғана, тек сонда ғана үздіксіз бейнелеу болады.

Дәлелі. f: T₁→T бейнелеу үздіксіз болсын, U^l T₂ -нің қандайда бір ашық жиыны болсын, яғни u 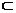Ф₂ болсын.

Біз барлық f(x) u¹ болатын x T нүктелер жиыны и- дың Т₁ -кеңістікте ашық жиын екенін, яғни u Ф, болатынын дәлелдейік.

U дан Х₀ нүкте алсақ f(x_o) u¹ болатындықтан f(x_o) нүкте үшін U^l аймақ болады. Шарт бойынша f бейнелеу Х₀ нүктеде үздіксіз болғандықтан Х₀ ден f(u_o) 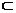u¹ болатын U _х аймағы болады. Онда u_x 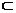u болады. Сондықтан U жиыны әрбір Х₀ нүктесімен қатар оның қандайда бір аймағында қамтиды.

Ал мұндай қасиетке тек ашық жиын ие болады. Демек и ашық жиын, сондықтан U 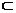Ф₁.

Керісінше f:T₁→ T₂ бейнеленуде ашық жиынның түп бейнесі ашық жиын болатын болсын. f -тің, Т₁ -дің әрбір нүктесінде үздіксіз болатынын дәлелдейік х₀ Т₁ нүкте алайық, f(x₀) нүкте аймағы U ¹ болсын. Шарт бойынша U ¹ тек түпбейнесі U жиыны Т₁ де ашық жиын болады.

x_o u, f(u) 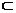u¹ болады. Анықтама бойынша бұл f бейнелеу Х₀ нүктеде үздіксіз деген сөз.

f:T₁→ T₂ топологиялық бейнелеу немесе гомеоморфизм делінеді егерде f өзара бір мәнді және өзара үздіксіз бейнелеу болса гомеоморфизм анықтамасынан, егер f: Т₁: Т₂ бейнелеу гомеоморфизм болса, онда f¹:T₂ →T₁ де гомеоморфизм болатынын және екі гомеоморфизімін көбейтіндісінде егер f¹:T₂ →T₁ гомеоморфизм болса онда Т₁ мен Т₂ өзара гомеоморфты делінеді, оны Т₁ ~ Т₂ деп жазады.

Гомеоморфты кеңістіктерді өзара топологиялы типтес дейді.

Топологиялық. қатыс эквивалиенттік қатыс болды, яғни топологиялық тұрғыда Т₁ мен Т₂ ші бір-бірімен өзгешілігі болмайды.

Топологиялық кеңістіктен гомеоморфизмде сақталатын қасиеттерін топологиялық қасиеттер дейді. Ондай қасиеттерді оқу геометриялық топология деп аталатын бөлімнің пәні болып табылады.

Екі топогиялық кеңістіктің гомеоморфты болар-болмасын ажырату үшін оның бірін екіншісіне көшіретін ең болмағанда бір гомеоморфизмнің болар-болмасына көз жеткізу керек, болса олар гомеоморфты, болмаса гомеоморфты емес болады.

Не нашли, что искали? Воспользуйтесь поиском: