Тополгиялық кеңістіктің класстары

Топологиялық кеңістіктің аса маңызды негізгі класстарына айырылатын компакты және байламды топологиялық кеңістіктер жатады.

Топологиялық кеңістіктің кезкелген әртүрлі екі нүктесінің қиылыспайтын аймағы болса, онда ол айырлатын толпологиялық кеңістік немесе хаусдорфты топологиялық кеңістік делінеді. (Хаусдорф (1868 – 1942ж) – топологиялық кеңісттік ұғымын алғаш ендірген неміс математигі).

Метрикалық, сандық, евклидтік, аффиндік, проективтік кеңістіктер айырылатын топологиялық кеңістіктер болады.

Мысалы a, b екі нүктенің арасы ρ (a, b) = z болса, ол нүктелердің 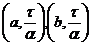аймақтары қиылыспайды. Ең болмағанда екі нүктесі болатын антидискреттік кеңістік айырылмайтын топологиялық кеңістік болады.

x жиынының, біріктірілмесі осы х жиынның өзі болатын, ішкі жиындарының жүйесі {x₂} сол х жиынның жабуы делінеді.

(Т,Ф) Топологиялық кеңістіктің жабуы { Т₂ } ашық делінеді, егер ішкі Т₂ жиындар ашық жиындар болса { Т₂ } жабудың өзіде жабу болатын ішкі үйірлерін оныңс бөлік жабуы дейді.

Егер топологиялық кеңістіктің әрбір ашық жабуы, ақырын санды бөлік жабулардан тұрса, онда ол компакты топологиялық кеңістік делінеді.

Топологиялық (Т,Ф) кеңістіктің х жиыны компакты делінеді, егер х ішкі кеңістік компакты болса.

Мысалы [ a,в ] сандық кесінді R сандық жиында компакты жиын болады. Сфера, шеңбер, үшбұрыш евклидтік кеңістікте компакты бөлік кеңістік болады. Бүкіл евклидтік, жазықтық, түзу компакты кеңістік болмайды. Евклидтік кеңістіктің жиыны компакты болу үшін ол тұйық және шектелген болуы керек.

Х жиынның жабуы сол жиынның бөлшектеулері делінеді. Егерде жабу элементтері бос жиын болмаса және жабудың кезкелген әртүрлі екім элементі қиылыспаса.

Топологиялық (Т,Ф) кеңістік байламды делінеді, егер оның екі ашық жиынға бөлшектеуі болмайтын болса.

Топологиялық (Т,Ф) кеңістіктің жиыны х байламды делінеді, егер ол Т- да байламды ішкі (бөлік) кеңістік болса.

Евклидтік, аффиндік, проективтік кеңістктер байламды топологиялық кеңістіктер болады. Сфера, элипс, жазықтық, түзу евклидтік жазықтықтың байламды ішкі жиындары болады. Ал, гипербола байламды жиын болмайды, өйткені оның әрбір тармағы бос жиын болады. Сөйтіп гипербола екі ашық жиынға бөлшектенеді.

Топологиялық кеңістіктегі айырылу компакты байламды болу қасиеттері топологиялық қасиетке жатады. Гомеоморфизм жәрдемімен бірі екіншісіне айналмайды. Олар әртүрлі топологиялық кластар жасайды.

52.2. Көпбейнелік. Toпологиялық (Т,Ф) кеңістіктің қандайда бір u ашық жиынын R^к санлық кеңістіктің ашық жиынынна топологиялық бейнелеу (гомеморфизм) φ сол (Т,Ф) кеңістіктегі К - өлшемді координаттық жүйе делінеді. Бұл кезде (u, φ) тұйық К -өлшемді карта U ол картаның координаталық аймағы делінеді. Егер x u болса онда оның бейнесі

φ(x) = (x₁, x₂, …, x_k) Є R^k мұндағы x₁, x₂, …, x_k сандары х -тың берілген картадағы координаттары делінеді.

Егер санаулы базасы айырлатын топологиялық кеңістікті К- өлшемді картаның координаттық аймағымен жабуға болса онда ол кеңістік К- өлшемді топологиялық көпбейнелік делінеді, К -ол топологиялық көпбейнеліліктің өлшемі делінеді және ол гомеморфизм де өзгермейді, топологиялық инвариант болады.

Біз тек 1,2 өлшемді топологиялық көпбейнеліктерді қарастырамыз.

Мысалы R^k=(k=1, k=2) сандық кеңістік санаулы бзасы айырылатын топологиялық кеңістік. Егер u= R^k, φ – бұл R^k - ны теңбе – тең түрлендіру десек (u, φ) K өлшемді карта болады. Сондықтан R^k K - өлшемді көпмүшелік болады. Дәл осы сияқты аффиндік А_к1 евклидтік Е_к проективтік Р_к кеңістіктерде К өлшемді көпбейнелік болады.

Мысал. Евклидтік Е₁ жазықтықта γ шеңбер берілсін. Оның центірі координата басы болатын О_ху тік бұрышты координата жүйеісн ендірейік. Шеңбермен у өсінің қиылысу нүктелерін А,В десек шеңбер радиусы I болсын (332-сурет).

Шеңберден А нүктені ойып алып тастағаннан қалған бөлігінт u₁= γ \ {A} ал В нүктені ойып алып тастағанннан қалған бөлігін u₂= γ\ {В } дейік.

y

A

M

x

N

B

332-сурет.

φ₁: U ₁→ O_x бейнелеуі U ₁ жиында АВ -ға перпендекуляр диаметрге А нүктеден центірлік проекциялау, ал φ₂: U → O_х бейнелеу U жиынды АВ -ға перпендекуляр диаметрге (яғни О_х өсіне) В нүктеден центірлік проекциялау болсын. Cонда φ₁(N)=N₀ , φ₂(M)=M₀ M_o N_o O_x болады. Бұл бейнелеулер U ₁, U ₂ ашық жиынды О_х ашық жиынға гомеоморфты бейнелеу боады.

Демек ( U ₁, φ₁), ( U ₂, φ₂) шеңберде анықталған бір өлшемді карталар (өйткені О_х осі R¹ түзу). Ол карталардың координаттық аймақтары U ₁ мен U ₂ берілген γ шеңберді толығымен жатады. Сондықтан шеңбер бірөлшемді көпбейнелік болады.

Жалпы кез келген байламды бір өлшемді компакты емес көпбейнелік түзуге, ол байламды бір өлшемді компакты көп бейнелік шеңберге гомеморфты болады.

Осы мысалдағы жолмен сфера евклидтік Е₃ кеңістікке екі өлшемді көп бейнелік болатындығын көрсетуге болады. Элипсоид, гиербололид, параболоид, цилиндрлерде 2 өлшемді көпбейнелік болады. Е₃ тің шектелген тұйық ішкі жиындары болғандықтан элипсоид сфера компакты, қалғандары компакт емес екі өлшемді көпбейнелік болады.

R^к (к=1,2) - дағы координаталары x^k ≥ 0 болатын нүкттелер жиынын R^к+ деп белгілесек, онда ол R^к – да тұйық жарты кеңістік болады.

(Т,Ф) Топологиялық кеңістік жиегі бар R өлшемді көпбейнелік делінеді, егерде ол 1-ден, айырылатын санаулы базалы кеңістік болса; 2-ден, оның нүктелері мынадай болатын екі классқа бөлуге болатын болса:

а) 1-класстың әрбір нүктесінің (олар ішкі нүктелер) R^к -ға гомеморфты аймағы болса.

б) 2-класстың әрбір нүктесінің (олар нүктелер) R¹₊ - ға гомеморфты болатын R^к -ға гомеморфты болмайтын аймағы болса.

Шекті нүктелердің жиынын көпбейнелік жиегі дейді (шеті, ернеуі деугеде болады).

Мысалы R¹, сандық жиынның [ a, b ] кесіндісі жиегі (шеті) а, b болатын бір өлшемді жиекті көпбейнелік болады.

Аффиндік А₃, евклидтік Е₃ кеңістікте кесінді тұйық сәуле бір өлшемді жиекті көпбейнелік болады. Кесіндінің жиегі оның екі ұшын, сәуленің жиегі оның бастапқы нүктесі болады.

Жалпы кез келген жиекті бір өлшемді көпбейнелік не кесіндіге, не тұйық сәулеге гомеморфты болады. Евклидтік жазықтықта дөңес көпбұрыш екі өлшемді жиекті көпбейнелік, ал тұйық жарты жазықтық екі өлшемді компакты емес жиекті көпбейнелік болады, оның жиегі жарты жазықтықты анықтайтын түзуі болады.

Егер евклидтік жазықтықтан АВСД тіктөртбұрышталып А мен Д,В мен С нүктелер беттесіндей етіп жапсырсақ (333-а, б сурет) шығады. Оның жиегі шеңберге гомеморфты екі γ₁, γ₂ фигуралардан тұрады. Бұл көпбейнелікті тұтқа дейді.

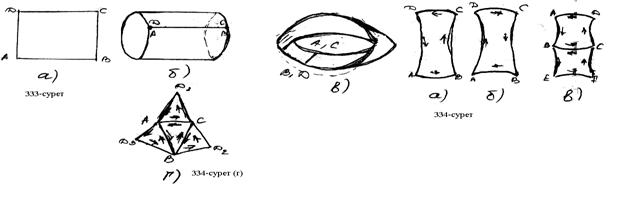
Егер АВСД тіктөртбұрыштың А мен С,В мен Д төбелері беттесетіндей етіп бұрап АД мен СД ны беттестіріп жапсырса 333-в сурет шығады. Оны Мёбиус жапырағы дейді. (А. Ф. Мёбиус (1790-1868) неміс математигі) ол жиегі шеңберге гомеморфты болатын екі өлшемді көпбейнелік. Мёбиус жапырағының ерекшелігі – ол бір жақты бет болады. Егер оны АВ -ға перпендекуляр бағытта кессе ол екіге бөлінбейді, бұрынғысынша байламды екі өлшемді көпбейнелік.

Дөңес көпбұрышқа гомеморфты болатын кезкелген көпбейнелікті клетка дейді (334-сурет)

Екі өлшемді Ғ көпбейнелік F₁, F₂, …, F_n клеткаларға жіктелген делінеді егер 1-ден, ол клеткалар Ғ -тың жабуы болса 2-ден, әртүрлі F_i, F _γ клеткалардың қимасы не бірқабырғадан, не бір төбеден тұрса, не бос жиын болса.

Кезкелген жиекті, жиексіз екі өлшемді компакты көпбейнеліктер әруақытта клеткаларға жіктеледі және бір неше жолмен жіктеледі. Егер клетканың бір қабырғасына бағыт берсе, онда ол қабырға бағдарланған делінеді. Сол арқылы барлық қабырғалар бағытталады.

Клетка екі түрлі бағдарлануы мүмкін. Сағат тілі қозғалысы бағытына қарсы (334-а сурет). Сағат тілі қозғалысы бағтында (334-б сурет).

Егер іргелес екі клетканың орта қабырғаларының бағдары бір-біріне қарама – қарсы болса (334-в сурет), онда ол екі клетка бірдей бағдарланған, кері жағдайда қарама – қарсы бағдарланған делінеді.

Егер көпбейнелікті әрбір іргелес клеткалары бағдарлас болатындай етіп клеткаларға жіктеуге болса, онда ол бағдарланатын кері жағдайда бағдарланбайтын көпбейнелік делінеді.

Не нашли, что искали? Воспользуйтесь поиском: