Исықтың негізгі мәселелері.

58.1. Қисықтың жанамасы.

а) Біз жатық сызықтарды қарастырамыз. Ол элементар сызық болмауы да мүмкін. L - жатық сызық М₀- онда жатқан нүкте болсын.Математикалық талдаукурсында L- қисықтың М₀ нүктедегі жанамасы деп М₀М қиюшының М нүкте сызық бойымен қозғалып М₀ нүктеге ұмтылған

L Z N u Z Mo

M₀ Mo m u

M L

L

T 0 y 0 y

M₀ x x

а) 366-сурет б) в)

кездегі оның шектік жағдайдағы М₀Т түзуін айтады (366-а сурет).

L сызығы, онда жатқан М₀- нүкте бұл нүктеден өтетін u түзуі, М₀М қиюшы берілсін. М₀ мен М нүктесі арасын d, М мен u түзуі арасын MN=h дейік. (366, б-сурет.) Сонда жанамаға жоғарыда берілген анықтамаға эквивалиенті мынадай анықтама беруге болады: u түзуі L сызықтың М₀ нүктедегі жанамасы делінеді, егерде м нүкте сызық бойымен М₀ нүктеге ұмытылғанда қатынас 0-ге ұмтылатын болса.

Бұл анықтама жанама бағытын анықтап, оның теңдеуін құруға көмектеседі.

б) Жатық L сызық O_xyz тікбұрышты координаталар жүйесінде параметрлік x=x(t), y=y(t), z=z(t) (58-1) теңдеумен берілсін.

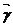Онда ранг y¹(t) x¹(t) z¹(t) =1 болу керек және бұл сызықтық векторлық теңдеуі (t)=x(t) + y (t) +z(t) 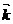болады (58-2)

Теорема L жатық сызығының теңдеуі (58-2) түрде болса онда ол сызықтың әрбір нүктесінде жанамасы болады және оның бағыттаушы векторы сол нүктедегі тунды вектор бағытымен бағыттас болады.

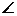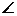Дәлелі: (58-2) теңдеумен берілген L —жатық сызықтың параметр t=t_o -ға сай келетін М₀ (t_o) нүктедегі жанамсы u түзуі болсын (366-б сурет). Ол түзудің бірлік бағыттаушы векторын делік М нүктеге t+Δt параметр сай келсін онда M₀M=d=| (t+Δt)- (t)|, MN=h= M₀Msin M M₀N= M₀M | | sin M M₀N= |M₀ |=|( (t+Δt)- (t)) t | болады.

(х-векторлық көбейту белгісі) сонда жанама анықтамасы бойынша мына қатынас Δt → 0 ұмтылғанда 0-ге ұмтылуы керек, яғни Δt →0 да (*) керек.

Ал, туынды ережесі бойынша бұл қатынас Δt → 0-ге ұмтылғанда мынадай болып шығады.

Бұл (*) бойынша 0–ге ұмтылады.

→ 0 бұдан = 0 Ал, бұл вектордың векторлық көбейту ережесі бойынша 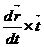мен коллинар болады деген сөз.

Сонымен М₀ нүктеден өтетін u түзуі жанама болса, оның бағыттаушы векторы сол нүктедегі туынды вектормен бағыттас болады екен.

Енді керісінше u түзуі М₀ нүктеден сол нүктедегі туынды бағытында жүргізілген түзу болсын.онда мұндай түзу үшін болады.

Ал, бұл түзу жанама болады деген сөз.

Сонымен жанаманың бағыты жанасу нүктедегі туынды бағытымен дәл келетіні дәлелденеді.

М₀ нүктеде туынды вектор біреу ақ болады. Сондықтан бұл нүктеден бұл бағытта бірақ түзу өтеді. Яғни әр нүктеден жүргізілген жанама біреуақ болады.

в) Жанама жүргізілетін нүкте мен оның бағыты белгілі болған соң. Ол жанаманың теңдеуі оп-оңай құрылады. = сызыққа оның М₀ (t_o) нүктесінен жүргізілген жанамасының теңдеуін құрайық. Ол u болсын жанама бойынан оның оның ағымдық М(t) нүктесін алайық оның радиус векторы 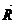={x, y, z}, М₀ нүктенің радиус векторы (t_o) болсыy. 366, в-сурет жанама векторы (t) -ға коллинар болатндықтан болады. Сонда суреттен болар еді.

Демек (58-3)

Мұны 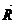={x, y, z}, |t_o|={x(t_o), y(t_o), z(t_o)}, |t_o|={x¹(t_o), y¹(t_o), z¹(t_o)} вектордың координаталары арқылы жазсақ.

(58-4) немесе (58-4а)

(58-3) Қисықтың векторлық (58-4, 4а) параметрлік теңдеуі делінеді.Егер y=y(x), z=z(x) теңдеумен берілсе оның параметрлік формасы

x=t, y=y(t), z=z(t) болдатындықтан, ол қиысқтың теңдеуі (58-4а) бойынша болады.

Егер қисық айқындалған теңдеумен берілсе

F(x(t), y(t), Z(t))=0, Ф(x(t), y(t), z(t))=0 теңбе-теңдіктен t арқылы туынды алсақ F_xx¹+F_yy¹+F_zz¹=0, Ф_xx¹+Ф_yy¹+Ф_zz¹=0 болар еді. Бұдан жанама

(t)= {x¹, y¹, z¹}, вектор бұл екі вектордың екеуіне де ортогонал болатынын көрінеді. Сондықтан вектор {F_x, F_y, F_z } {Ф_x, Ф_y, Ф_z } вектордың векторлық көбейтіндісіне коллинеар болады. Сондықтан оның координаталары мынадай болады.

(58-6а)

Демек бұл кездегі жанама теңдеуі мынадай болады.

(58-6б)

58.2 Қисық доғасының ұзындығы. С^к классты жатық L сызығы параметрлік формада x=x=(t), y=y(t), z=z(t) (58-1) теңдеумен берілсін.

Оның бойынан to және t параметрлерге сай келетін A(t_o), B(t) нүктелер алайық (367-сурет) сонда АВ доағаның ұзындығы деп, оны іштей сызылған T₀T₁, T₁T₂, …, T_n-1T_n сынық сызықтар периметрінің сынық сызық саны шексіз көбейгендегі (ең үлкен сынық сызық ұзындығы 0-ге ұмтылғандағы ұмтылатын шегін айтады (367-сурет)

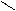T_nb

T_n-1

T₂

A T₁

367-сурет

Хорда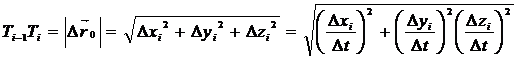

Егер онда болатындықтан мұны f_i (t_i) дейік.

Айнымалы шегі мен шексіз кіші шаманың қосындысына тең болатындықтан болады. Сонда сынық сызықтар параметрі болады. Мұның бірінші қосылғышы f(t_i) функцияның интегралдық қосындысы, ал екіншісі n → ∞ ұмтылғанда 0-ге ұмтылады. Сондықтан n → ∞ етіп шекке көшсек.

Сонымен басы t_o, саны айнымасы t параметрге сай келетін доға ұзындығы мына формулалармен анықталады екен.

(58-7a) 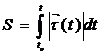(58-7б)

Доға ұззындығы t-ның функциясы болады екен.

Сондықтан 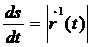(58-8)

Сонда доға дефференциалы

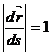(58-9) бұдан (58-10) дан (58-11)

Сонымен доға ұзындығы параметр үшін алынса, онда бірлік вектор болады екен. Ал, мұның геометриялық мәні хор даның оған керілген доғаға қатынасының шегі 1-ге тең болады (доға 0-ге ұмтылғанда) дегенді білдіреді. S -ті натурал немесе табиғи параметр дейді.

Егер қисық y=y(x), z=z(t) теңдеумен берілсе онда x=x(t), y=y(t), z=z (t) болатындықтан доға ұзындығы (58-12) формуламен табылатын болады.

Ескерту: жалпы параметр t мен алынған туындыларды , , деп белгіледік. Ал қисық табиғи S параметр мен = (s) болып берілс, онда , ,

Не нашли, что искали? Воспользуйтесь поиском: