
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Френс үш жағы элементтерінің теңдеулері
1- жағдай. Қисық табиғи параметр S арықылы берілсін
 =
=  (S) = x(s)
(S) = x(s)  +y(s)
+y(s) 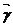 +z(s)
+z(s) 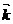 (58-13)
(58-13)
Онда  ол қисық жанама болады.
ол қисық жанама болады.
Сондықтан қисық жанамасының бағыттаушы векторы  болады. Бас нормал векторы
болады. Бас нормал векторы  болтын сондықтан бос бас нормалдың бағыттаушы векторы
болтын сондықтан бос бас нормалдың бағыттаушы векторы
 (*2) болады. Бинормалдың брлік векторы
(*2) болады. Бинормалдың брлік векторы  болғандықтан бинормалдың бағыттаушы екторы мынадай болады.
болғандықтан бинормалдың бағыттаушы екторы мынадай болады.
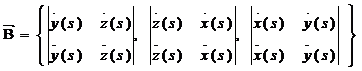 (3*)
(3*)
Сонда Қисықтың Mo (x(to), (y(to), (z(to), нүктесінен жүргізілген жанамалың теңдеуі мынадай болады.
а)  (58-18)
(58-18)
б) Бас нормалдың теңдеуі мынадай болады  (58-20)
(58-20)
в)  жанама вектор мен
жанама вектор мен  векторларға паралель болатындықтан жанасу жазықтығының теңдеуі мынадай болады.
векторларға паралель болатындықтан жанасу жазықтығының теңдеуі мынадай болады.  (58-21)
(58-21)
г) Жанама  векторға перпендикуляр болғандықтан нормал жазықтың теңдеуі мынадай болады.
векторға перпендикуляр болғандықтан нормал жазықтың теңдеуі мынадай болады.  (58-22)
(58-22)
д) Бас нормалға  перпендикуляр болғандықтан түзуленетін жазықтық теңдеуі мынадай болады.
перпендикуляр болғандықтан түзуленетін жазықтық теңдеуі мынадай болады.  (58-23)
(58-23)
2- жағдай. Қисық жалпы параметр t мен берілсін.
 (58-24)
(58-24)
Бұл кезде  вектор қисыққа жанама болады. Сондықтан қисық жанама сынық бағыттаушы векторы
вектор қисыққа жанама болады. Сондықтан қисық жанама сынық бағыттаушы векторы  болады, бірақ векторы
болады, бірақ векторы  (1ll*)
(1ll*) 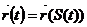 дейміз. Сонда (11*)
дейміз. Сонда (11*)  болады. Бұдан
болады. Бұдан  болады.
болады.
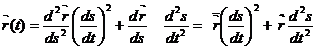
Демек  вектор
вектор 
 векторларға жіктелгендіктен олар бір жазықтықта жатады. Ал,
векторларға жіктелгендіктен олар бір жазықтықта жатады. Ал,  пен
пен  жанасу жазықтықтарында жатады. Сондықтан
жанасу жазықтықтарында жатады. Сондықтан  векторды жанасу жазықтығында жатады,
векторды жанасу жазықтығында жатады,  болғандықтан векторда сол жазықтықта жатады. Ал, бинормал вектор жанасу жазықтығына перпендекуляр болатын. Сондықтан бинормал бинормал векторы
болғандықтан векторда сол жазықтықта жатады. Ал, бинормал вектор жанасу жазықтығына перпендекуляр болатын. Сондықтан бинормал бинормал векторы 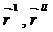 векторлардың векторлық көбейтіндісі мен каллинор болады, яғни
векторлардың векторлық көбейтіндісі мен каллинор болады, яғни  болады. Сондықтан
болады. Сондықтан  дейік.
дейік.
Мұның бірлік векторы 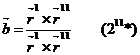
Сонда бас нормалдың бағыттаушы векторы  дейік (31*)
дейік (31*)
Бірлік вектор  (311*)
(311*)
Сонымен жалпы параметр t кезде жанам түзудің бағыттаушы векторы  ={x1(t), y1(t), z1(t), } болады. Бос нормалдың бағыттауыш векторы
={x1(t), y1(t), z1(t), } болады. Бос нормалдың бағыттауыш векторы
 { a1,a2,a3 } болады.
{ a1,a2,a3 } болады.
Бинормалдық бағыттауыш векторы  ={ b1, b2, b3 } болады.
={ b1, b2, b3 } болады.
Жанама вектордың бірлік векторы  формуламен табылады.
формуламен табылады.
Бас нормалдың бірлік векторын 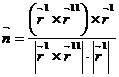 формуламен табылады.
формуламен табылады.
Бинормалдың бірлік векторы  формуламен табылады.
формуламен табылады.
Сондықтан жалпы параметрмен берілген кедегі M0 (x(to), (y(to), (z(to), нүктеден жүгізілген
а) Жанама түзудің теңдеуі  (57-181)
(57-181)
б) Бас нормалдың теңдеуі  (57-191)
(57-191)
в) Бинормалдың теңдеуі  (58-201)
(58-201)
г) Жанасу жазықтығы жанама түзу мен бас нормалға паралель болатындықтан оның теңдеуі мынадай болады.  (58-21)
(58-21)
д) Нормал жазықтық жанама түзуге перпендекуляр болғандықтан оның теңдеуі мынадай болады. x1(t) (x0-x0 (t1) + (y-y0 (t)) y01+(z-zv(t))zv1(t)=0 (58-221)
е) Түзуленетін жазықтық жанама түзумен бинормалға паралель болатындықтан оның теңдеуі мынадай болады.
 (58-231
(58-231
Ескерту: Бұл теңдеулерді құруда Mo(xo: yo: zo) нүктеден  вектор бағытында өтетін түзу теңдеуі
вектор бағытында өтетін түзу теңдеуі  болатынын және
болатынын және
Mo(xo, yo, zo) нүктеден  векторы перпендекуляр етіп жүргізілетін жазықтық теңдеуі a1(x-xo)+ a2(y-yo)+ a3(z-zo)=0 болатынын және
векторы перпендекуляр етіп жүргізілетін жазықтық теңдеуі a1(x-xo)+ a2(y-yo)+ a3(z-zo)=0 болатынын және
Mo(xo, yo, zo) нүктеден 
 векторларға паралель етіп жүргізілген жазықтық теңдеуі мынадай
векторларға паралель етіп жүргізілген жазықтық теңдеуі мынадай
(57-181)  болатыны ескеріледі.
болатыны ескеріледі.
Френс формулалары
Қисық бойымен М нүкте қозғалғанда ол нүктеден жүргізілген Френс үшжағаның бірлік векторлары  ,
, 
 өздерінің бағыттарын өзгертеді. Сол өзгерістерді бұл векторлардан алынған туындылар
өздерінің бағыттарын өзгертеді. Сол өзгерістерді бұл векторлардан алынған туындылар  ,
, 
 сипаттайды сондықтан осы векторларды табайық, яғни оларды
сипаттайды сондықтан осы векторларды табайық, яғни оларды  ,
, 
 векторларға жіктейік бас нормал түзуінің бағыттаушы векторының бірлік векторы
векторларға жіктейік бас нормал түзуінің бағыттаушы векторының бірлік векторы  еді. Бұдан S арқылы туынды алсақ бұл бірлік вектор болғандықтан өзінің туындысына перпендекуляр болады.
еді. Бұдан S арқылы туынды алсақ бұл бірлік вектор болғандықтан өзінің туындысына перпендекуляр болады. 
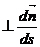
Ал  векор түзуленетін жазықтыққа перпендекуляр еді. Сондықтан
векор түзуленетін жазықтыққа перпендекуляр еді. Сондықтан  түзуленетін жазықтықта жатады. Сөйтіп
түзуленетін жазықтықта жатады. Сөйтіп  мен
мен  ға компланар болады. Былайша жіктелген
ға компланар болады. Былайша жіктелген
 = α
= α  +β
+β  (*)
(*)
Мына  ·
·  =0 теңбе теңдікті S арқылы дифференциалдасақ
=0 теңбе теңдікті S арқылы дифференциалдасақ  ·
·  +
+ 
 =0 болады. Орындарына қойсақ
=0 болады. Орындарына қойсақ  Бұған(*) мен
Бұған(*) мен  = k
= k  орындарына қойсақ:
орындарына қойсақ:
k 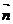 ·
· 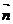 +
+  (α
(α  + β
+ β  )=0 бұдан α=-k
)=0 бұдан α=-k
Сонда (58-24)  =-k
=-k  + β
+ β  (58-24а)
(58-24а)
 =
= 

 еді, мұны S арқылы дифференциалдасақ
еді, мұны S арқылы дифференциалдасақ  =
= 

 +
+ 

 бұған
бұған  мен
мен  мәндерін қойып
мәндерін қойып
 =k
=k 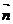

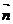 +
+ 
 (-k
(-k  +β
+β  )= k
)= k 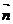 x
x 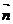 -k
-k 

 +β
+β 

 =0-0-β
=0-0-β 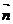
 =-β
=-β 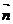 (58-24б)
(58-24б)
Сонымен  =k
=k 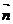
 =k
=k 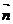
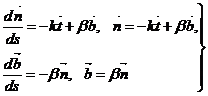 (58-24)
(58-24)
Бұларды сәйкесінше, Френенің бірінші, екінші, үшінші,формулалары дейді.
Мұны  =o
=o  +k
+k  +o
+o 
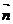 =-k
=-k  +o
+o 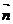 +β
+β 
 =ot-β
=ot-β 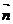 +o
+o 
деп жазсақ, матрицасы  болады.
болады.
Не нашли, что искали? Воспользуйтесь поиском: