
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ені скаляр аргументті вектор – функция.
Евклидтік Е3 кеңістікте нақты сандар жиыны R -де анықталған үш өлшемді V3 векторлық – кеңістік шешімді және екі өлшемді Д аралық (яғни мына үш жиынның бірі.
а) R2=R  R кеңістік, бұл (х,у) нүктелер жиыны);
R кеңістік, бұл (х,у) нүктелер жиыны);
б) R+ сандық тұйық жарты кеңістік (яғни v ≥ 0 болатын (u, v) ЄR2 нүктелер жиыны);
в) сандық квадрат (яғни 0 ≤ u ≤ a, 0 ≤ u ≤ a, a>0 болатын (u, v) ЄR2 нүктелр жиыны) берліген.
Егер Д аралаықтың әрбір (u, v) нүктесіне V3 векторлық кеңістіктің бір  векторлы сәйкестенділетін ерже немесе заң белгілі болса, онда екі өлшемді Д аралықты u, v екі скаляр аргументті вектор – функция
векторлы сәйкестенділетін ерже немесе заң белгілі болса, онда екі өлшемді Д аралықты u, v екі скаляр аргументті вектор – функция  =
=  (u, v) берілген делінеді.
(u, v) берілген делінеді.
Егер V3 -тен ( )орта нормалнған базис алайық,
)орта нормалнған базис алайық,  (u, v) вектор базистік векторларға жікелер еді және жіктелу коэффициенттері х, у, z сандары (u,v) нүкте Д аралықта жүріп өткенде өзгреді. Яғни олар u, v-ның функциялар болады. Сөйтіп |
(u, v) вектор базистік векторларға жікелер еді және жіктелу коэффициенттері х, у, z сандары (u,v) нүкте Д аралықта жүріп өткенде өзгреді. Яғни олар u, v-ның функциялар болады. Сөйтіп |  (u,v)=x(u,v)
(u,v)=x(u,v) 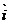 +y(u,v)
+y(u,v)  +z(u,v)
+z(u,v) 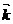 (59-1) болады.
(59-1) болады.
Мұндағы x(u,v), y(u,v), z(u,v) скаляр функцияларды вектордың базистегі координаталары дейді.
Егер (u,v) үшін нүкте (u0,v0) нүктеге ұмтылғанда  (u,v) -
(u,v) -  (a1, a2, a3) айырым шексіз кіші болса, онда тұрақты
(a1, a2, a3) айырым шексіз кіші болса, онда тұрақты  {a1, a2, a3} векторы
{a1, a2, a3} векторы  (u,v) вектор - функцияның шегі делінеді және ол былайша жазылады:
(u,v) вектор - функцияның шегі делінеді және ол былайша жазылады:

Мұндай шектің болуы үшін
 ,
,  ,
,  шектің болуы керек
шектің болуы керек
Егер  болса, онда
болса, онда  =
=  (u,v)
(u,v)
Вектор (u0,v0) нүктеде үздіксіз делінеді. Вектор Д аралықта үздіксіз болу үшін, ол жиын әрбір нүктелрді үздіксіз болуы керек. Егер u мен v -ның бірі тұрақты болып (мысалы v=v0 тұрақты) екіншісі ғана Д аралықта өзгерсе, онда  (u,v0) функция бұл аралықта бір аргументті фуекция болады. Осы кезде
(u,v0) функция бұл аралықта бір аргументті фуекция болады. Осы кезде  (u, v0) туынды бар болды, онда oны
(u, v0) туынды бар болды, онда oны  (u,v) вектор функцияның (u0, v0) нүктедегі u арқылы алынған дербес туындысы делінеді де
(u,v) вектор функцияның (u0, v0) нүктедегі u арқылы алынған дербес туындысы делінеді де 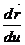 немесе
немесе  u арқылы белгілейді. Егер u=u0 тұрақты болып v өзгерсе
u арқылы белгілейді. Егер u=u0 тұрақты болып v өзгерсе  туындыны
туындыны
 (u,v) вектр дифференциялы v арқылы алынған дрбес тундысы дейді де
(u,v) вектр дифференциялы v арқылы алынған дрбес тундысы дейді де 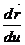 немесе
немесе  v арқылы белгілейді.
v арқылы белгілейді.
(59-1) ден  (u, v0)={x(u, v0), y(u, v0), z(u, v0)} және
(u, v0)={x(u, v0), y(u, v0), z(u, v0)} және
 (u0,v)={ x(u0,v), y(u0,v), z(u0,v)} болатыны шығады. Сондықтан
(u0,v)={ x(u0,v), y(u0,v), z(u0,v)} болатыны шығады. Сондықтан  u,
u,  v дербес туындылар бар болу үшін
v дербес туындылар бар болу үшін 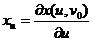 ,
, 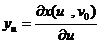 ,
, 
және  ,
,  ,
, 
Туындылардың болуының шығады..
Бұл кезде  u=xu
u=xu 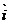 +yu
+yu  +zu
+zu 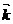 ,
,  v=xv
v=xv 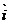 +yv
+yv  +zv
+zv 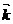 (59-2) болады.
(59-2) болады.
(59-1) дегі x(u,v), y(u,v), z(u,v) функциялар (u,v)  D нүктеде дифференцианалданатын функциялар болса, онда мынадай болады:
D нүктеде дифференцианалданатын функциялар болса, онда мынадай болады:
d  =dx(u,v)
=dx(u,v) 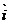 +dy(u,v)
+dy(u,v)  +dz(u,v)
+dz(u,v) 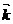 (59-3)
(59-3)
Бұл  (u,v) функцияның (u,v) нүктедегі дифференциалы делінеді. Мұны (59-2) былай жазуға болад:
(u,v) функцияның (u,v) нүктедегі дифференциалы делінеді. Мұны (59-2) былай жазуға болад:
d 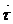 (u,v)=
(u,v)=  udu+
udu+  vdv (59-3a)
vdv (59-3a)
 (u,v) функция (u,v) нүктеде диференциалданатын функция болу үшін
(u,v) функция (u,v) нүктеде диференциалданатын функция болу үшін
{ x(u,v), y(u,v), z(u,v) } функциялар срол нүктеде диференциалданатын функциялары болуы керек.
Егер  (u,v) Д аралықтың әрбір нүктесінде диференциалданатын функция болса, оны Д аралықта диференциалданатын функция дейді.
(u,v) Д аралықтың әрбір нүктесінде диференциалданатын функция болса, оны Д аралықта диференциалданатын функция дейді.
Не нашли, что искали? Воспользуйтесь поиском: