
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Бет туралы түсінік.
а) Егер Евклидтік Е2 жазықтыққа Оху координаты жүйесін ендірсек, онда Е2 жазықтықтың әрбір М(х,у) нүктесіне R2 (х,у) саны (нүктесі) сәйкестенеді және бұл Е2 → R2 сәйкестік гомеоморфизм болады. Сондықтан R2 сандық кеңістігіне Е2 жазықтықпен, R2+ сандық жарты кеңістікті у 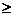 0 болатын жарты тұйық жазықтықпен, ал қабырғалары а болатын сандық квадратта төбелері O(o;o), A(a; a), C(c; c) В(o, a) болатын ОАСВ квадратпен теңестіруге (теңбе – тең деп қарастыруға) болады. Евклидтік Е3 кеңісті жазықтықты тұйық жарты жазықтықты, квадратты қарапайым бет дейді.
0 болатын жарты тұйық жазықтықпен, ал қабырғалары а болатын сандық квадратта төбелері O(o;o), A(a; a), C(c; c) В(o, a) болатын ОАСВ квадратпен теңестіруге (теңбе – тең деп қарастыруға) болады. Евклидтік Е3 кеңісті жазықтықты тұйық жарты жазықтықты, квадратты қарапайым бет дейді.
б) Қарапайым беттердің біріне гомеоморфты болатын фигураны элементар бет дейді. Мысалы, жазықтыққа гомеоморфты болғандықтан элипстік, гиперболалық параболойдтар, параболалық цилиндрлер элементар бет болады. Дөңгелекке гомеоморфты болғандықтан (ал дөңгелек квадратқа гомеоморфты) ернеуі (жиегі) бар жарты сфера да элементар болады. Жоғарыда айтылған себептерден екі өлшемді Д сандық аралықтарға гомеоморфты болатын кезкелген кеңістік фигурасы элементар бет деуге болады.
в) Санаулы не шектеулі элементар беттермен жабуға болатын кеңістік фигурасы F -ты бет (толық бет) дейді. Демек F бет, ал М -оның нүктесі болса, онда M  F0
F0 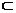 F болатын F0 элементар беттің болуы (табылуы) керек. Сфера (оны екі жарты сферамен жабуға болады), эллипстік цилиндр (оны санаулы цилиндрлік жолақтармен жабуға болады) бет болады, бірақ олар қарапайым беттердің ешқайсысына гомеоморфты болмайтындықтан элементар бет болмайды. Екі қуысты гипербалоид, гиперболалық цилиндр де бет болады.
F болатын F0 элементар беттің болуы (табылуы) керек. Сфера (оны екі жарты сферамен жабуға болады), эллипстік цилиндр (оны санаулы цилиндрлік жолақтармен жабуға болады) бет болады, бірақ олар қарапайым беттердің ешқайсысына гомеоморфты болмайтындықтан элементар бет болмайды. Екі қуысты гипербалоид, гиперболалық цилиндр де бет болады.
г) F беттен М нүктесі оның кәдімгі (жай) нүктесі делінеді егер де ол нүктенің F -пен қимасы F  W(M,ε) элементар бет болатын W(M, ε)1 аймағы болса. Егер бұл қима жазықтыққа (тұйық жарты жазықтыққа) гомеоморфты болса ол нүкте ішкі нүкте (шекаралық нүкте) делінеді кәдімгі (жай) емес нүктені айрықша нүкте дейді.
W(M,ε) элементар бет болатын W(M, ε)1 аймағы болса. Егер бұл қима жазықтыққа (тұйық жарты жазықтыққа) гомеоморфты болса ол нүкте ішкі нүкте (шекаралық нүкте) делінеді кәдімгі (жай) емес нүктені айрықша нүкте дейді.
Мысалы, 371-суреттегі цилиндрлық бет өзін-өзі MN түзуі бойымен қияды. Ол түзу бойындағы кезкелген нүкте айрықша нүкте болады.

 M
M
 | |||
 |


N 371-сурет
Барлық нүктесі кәдімгі нүкте болатын бетті жай бет дейді, беттің шекаралық нүктелерінің жиыны оның шекарасы (жиегі, ернеуі, шеті) дейді. Кезкелген элементар бет жай бет болады.
Мысалы сфера, эллипсоид, эллипстік цилиндр гиперболоид жай бет болады. Конус жай бет болмайды, өйткені оның төбесі айрықша нүкте болады, квадратқа гомеоморфты болатын кезкелген бет жиекті шеңберге гомеоморфты болатын жиекті бет болады. Тұйық жарты жазықтыққа гомеоморфты болатын кезкелген бет те жиекті бет болады, бірақ мұның жиегі түзуге гомеоморфты болады. Біз көбінесе жай F бетті оның M нүктесінің W(M, ε) аймағында қарастырамыз. Аймақ радиусы Е -ні барынша кіші етіп алу арқылы F  W(M, ε) қиманы жазықтыққа немесе ашық дөңгелекке гомеоморфты болатындай етуге болады.
W(M, ε) қиманы жазықтыққа немесе ашық дөңгелекке гомеоморфты болатындай етуге болады.
Алдағы кезде Д -деп жазықтыққа (R2 сандық кеңістікке) гомеоморфты жащық облысты, F0-деп Д -ға гоммеоморфты F  W(M, ε) элементар бетті белгілейміз. Д аралыққа u,v комплексті жүйесін, ал кеңістікке Охуz тікбұрышты координаталар жүйесін ендіріп, Д облысты F 0 элементар бетке белгілейтін f: D → Ғ0 гомеоморфизмді қарастырайық (372-сурет)
W(M, ε) элементар бетті белгілейміз. Д аралыққа u,v комплексті жүйесін, ал кеңістікке Охуz тікбұрышты координаталар жүйесін ендіріп, Д облысты F 0 элементар бетке белгілейтін f: D → Ғ0 гомеоморфизмді қарастырайық (372-сурет)


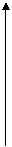
 v D
v D






|





 lv
lv 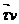
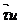
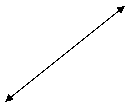

 lu
lu
 |
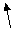
 z
z
 u x 0 y u
u x 0 y u
372-сурет
Бұл гомеоморфизмде M(u,v) ε D нүкте M(х,у,z) нүктеге көшетін болса, онда х,у,z координаталар Д облыста анықталған үздіксіз функцмясы болады.
x=x(u,v), y=y(u,v), z=z(u,v) (59-4)
Мұнда F0 бейнелігінің параметрін теңдеуі дейді. Бұл теңдеулер жүйесі мынадай бір вектор функциямен эквивалиенті болады:
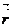 (u,v)= x(u,v)
(u,v)= x(u,v) 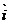 +y (u,v)
+y (u,v)  +z (u,v)
+z (u,v) 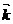 (59-5)
(59-5)
Міне осы 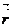 =
= 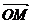 вектордың ұшы M нүкте берілген F 0 беттті жасайды.
вектордың ұшы M нүкте берілген F 0 беттті жасайды.
д) (59-4) теңдеумен берілген Ғ0 элементар бет Ск классты жатық (жылтыр, тегіс) бет делінеді, егерде ол теңдеудегі x(u,v), y(u,v), z(u,v) функциялар Д облыста k -рет үздіксіз дифференциалданатын болса және Д -ның әрбір (u,v) нүктесінің мына матрицаның 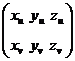 рангы 2-ге тең болса:
рангы 2-ге тең болса:
ранг 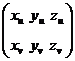 =2 (59-6).
=2 (59-6).
Жай бет F Ск классты жатық (жылтыр, тегіс) бет делінеді. Егер оның әрбір ішкі нүктесі М -нің F бетпен қимасы F  W(M, ε) Ск – классты жатық (элементар) бет болатын W(M, ε) аймағы табылатын болса
W(M, ε) Ск – классты жатық (элементар) бет болатын W(M, ε) аймағы табылатын болса
(59-5) тен  u = xu
u = xu  + yu
+ yu  +zu
+zu  ;
;  v=xv
v=xv 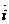 +yv
+yv  +zv
+zv 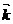 (59-7).
(59-7).
Демек (59-6) шарты геометрияда Д облыста  u,
u,  v векторлар сызықтық тәуелсіз болады, яғни
v векторлар сызықтық тәуелсіз болады, яғни 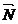 =
=  u
u 
 v векторлық көбейтінді Д- ның кезкелген нүктесінің 0-ге тең болмайды дегенді білдіреді.
v векторлық көбейтінді Д- ның кезкелген нүктесінің 0-ге тең болмайды дегенді білдіреді.
Егер (59-4) –те v=v0 тұрақты болып Д -да и -ғана өзгеретін болса, онда
 (u,v) <
(u,v) <  (u,v0) бір скаляр аргументті функция болады да
(u,v0) бір скаляр аргументті функция болады да  (u,v0) =
(u,v0) = 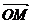 вектордың ұшы М нүкте F0 бетте жататын бір жатық сызық сызар еді. Оны u - сызығы дейді, оған
вектордың ұшы М нүкте F0 бетте жататын бір жатық сызық сызар еді. Оны u - сызығы дейді, оған  u вектор жанама болады. Осы сияқты
u вектор жанама болады. Осы сияқты  (u0,v) вектроларының ұшы да F – бетте бір жаттық сызық сызар еді. Оны v- сызығы дейді, оған
(u0,v) вектроларының ұшы да F – бетте бір жаттық сызық сызар еді. Оны v- сызығы дейді, оған  v вектор жанама болады. Әрбір (u,v)
v вектор жанама болады. Әрбір (u,v)  D нүктеге M(x,y,z)
D нүктеге M(x,y,z)  F0 нүкте сай келетіндіктен (u,v) параметрлерді М нүктенің F0 беттегі сызықтық координаталары дейді.
F0 нүкте сай келетіндіктен (u,v) параметрлерді М нүктенің F0 беттегі сызықтық координаталары дейді.
(59-4) теңдеу f: D → F0 гомеоморфизмді тудыра тудыратындықтан (яғни бейнелеу үздіксіз және өзара бірмәнді болғандықтан) и сызықтар үйірі бірімен-бірі қиылыспайтын сызықтар болады, v -сызықтар үйірі де өзара қиылыспайтын сызықтар болады, v -сызықтар үйірі де өзара қиылыспайтын сызықтар болады. Сөйтіп F0 бетте қисық сызықтар қатарын жасайды. Оларды координаттық тор дейді (372-сурет). Ол тор екі түрлі сызықтар үйірінен тұрады және олар F0 -дың әр нүктесінен бір-біреуден өтетіндей болып F0 -ды толығымен жауып жатады.
е) Егер бет z=f(x, y), x,y  D теңдеумен берілсе, онда оны (u,v) параметр арқылы былайша x=u, y=v, z=f(u,v) жазуға болатындаықтан және мұндай теңдеу Ск классты жатық бетті анықтау үшін бұл теңдеулердің оң жағындағы функциялар k -ретке дейін үздіксіз дифференцияналданатын функциялар болулары керек еді. Сондықтан z=f(x, y) теңдеу Ск классты жатық бетті анықтау үшін f(x, y), функцияның Д облыста k-ретке дейінгі туындылары болуы керек.
D теңдеумен берілсе, онда оны (u,v) параметр арқылы былайша x=u, y=v, z=f(u,v) жазуға болатындаықтан және мұндай теңдеу Ск классты жатық бетті анықтау үшін бұл теңдеулердің оң жағындағы функциялар k -ретке дейін үздіксіз дифференцияналданатын функциялар болулары керек еді. Сондықтан z=f(x, y) теңдеу Ск классты жатық бетті анықтау үшін f(x, y), функцияның Д облыста k-ретке дейінгі туындылары болуы керек.
Мысалы 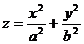 элипстік параболаид
элипстік параболаид  классты жатық бет болады.
классты жатық бет болады.
ж) Кеңістікте координаталары Ф(x, y, z)=0 теңдеуді қанағаттандыратын нүктелер жиыны F берілсін. Қандай жағдайда бұл теңдеу жатық бетті анықтайды деген сұраққа математиканың талдау курсында қарастырылатын айқындалмаған функция жайлы мына теорема жауап береді.
Теорема. F -тің M0(x0, y0, z0) нүктесі төмендегідей екі талапты қанағаттандырса
1. бұл нүктенің қандай да бір аймағында Ф(х,у,z) функциясының өзі және оның дербес туындылар Фх, Фу, Фz үздіксіз болса;
2. М0 нүктедегі Фх, Фу, Фz – терден жасалған матрица рангы.
Ранг (Фх, Фу, Фz) = 1 –ге тең болса онда М0 нүктенің W0  W0 аймағы табылып W10
W0 аймағы табылып W10  Ф қима Ск - классты жатық бет болады.
Ф қима Ск - классты жатық бет болады.
Мысалы x2+y2+z2  2=0,
2=0, 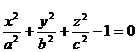 теңдеулерді координаталары қанағаттандырылатын нүктелер жиыны (бұл жиындар сфера мен элипсоид болады) жатық бет болады. Өйткні бұл теңдеулер жоғарда айтылған екі талапты да қанағаттандырады. Демек сфера элипсоид жатық бет болады.
теңдеулерді координаталары қанағаттандырылатын нүктелер жиыны (бұл жиындар сфера мен элипсоид болады) жатық бет болады. Өйткні бұл теңдеулер жоғарда айтылған екі талапты да қанағаттандырады. Демек сфера элипсоид жатық бет болады.
Не нашли, что искали? Воспользуйтесь поиском: