Беттің жанама жазықтығы мен нормалы

а) D 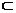R² облыста = (u,v) (59-8) теңдеумен С^к- классты жатық бет F берілсін.

u=u(t), v=v(t) (59-9) -дейік

Мұндағы t параметр I 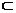R аралықта (u(t), v(t)) Д- да жататындай болып өзгеріп және бұл аралықта u(t), v(t) функциялар k- ретке дейін дифференциалданатын болсын және , туындылар I аралықта қатарына 0-ге тең болмайтын болсын мұны (59-8)- ге қойсақ

= (u(t), v(t)) (59-10) шығады.

Бұл бір t аргументті вектор – функция. Сондықтан ол F бетте жататын С-^к классты жатық сызықты анықтайды. Сөйтіп (59-9), (59-10) бетте жатқан С^к- классты жатық сызықтық теңдеулері болады.

Егер М₀ (u₀, v₀) бет F -те жатса онда бұл нүктеден шексіз көп сызықтары өтеді. Oл сызықтарға М₀ нүктеден жүргізілген жанамалар жиынын F беттен М₀ нүктедегі контингенциясы дейді. Егер беттен М₀ нүктедегі контингенциясы бір жазықтықта жатса ол жазықтықта бетке сол нүктедегі жанама жазықтық делінеді. Ол жазықтыққа сол М₀ нүктеден жүргізілген перпендекуляр түзуді, F беттен М₀ нүктедегі нормаль дейді.

Теорема. Егер F (59-8) теңдеумен берілген С^к -классты жатық бет, М₀ M₀ (u₀, v₀) ол бетте жатқан нүкте болс, онда бұл беттегі М₀ нүктесінен өтетін қисықтарына осы нүктеден жүргізілген жанамалар жиыны (М_{0 u}, _v) жазықтықта жататын М₀ центірі түзулер шоғын жасайды.

Дәлелі F бетте жататын L сызық М₀ нүктеден өтсін. Ол нүктеге параметрдің t мәні сәйкес келсін. Яғни u₀=u(t₀), v₀=v(t₀), болсын. Бұл сызыққа М₀ нүктеден жүргізілген жанама векторды анықтау үшін (59-10) теңдеуден t арқылы туынды алу керек.

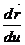
= + = _u + _v

Мұнда _{u, v} векторлар M₀ (u₀, v₀) нүктеде , туындылар t₀ нүктеде есептелген.

Соңғы теңдік , _{u v} векторларды сызықтық тәуелді болатынын яғни копмлонор болатынын көрсетеді.сондықтан олар (M₀, _{u v},) жазықтықта жатады. Мұндағы L сызықта жанама вектор, ал _{u v} сол жанасу нүктеден өтетін u -сызық пен v -сызыққа жанама векторлар.

Сонымен бетте жатқан сызықтың жанамасы _u мен _v және М₀ жатқан жазықтықта жатады екен.

Енді керісінше М₀ нүктеден өтетін _u, _v, М₀ мен анықталатын жазықтық та жататын қандайда бір бетін жатқан сызықтың жанамсы болатынын дәлелдейік.

(М₀ ) беттен М₀ нүктесінен өтетін (М₀, _u, _v) жазықтықта жататын түзу болсын. Онда =α _u+β _v (*) болып жіктеледі. Мынадай теңдеумен.

u=u₀+ αt, v=v₀+βt (*,*) берілген

L * сызығын қарастырайық. Сонда бұл сызықтың векторлық теңдеуі 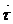= (u₀+ αt, v₀+ βt) болады. Бұған М₀ нүктеде жанама болатын вектор = _u + _v болады, ал (**) дан = α, = β болатындықтан = ^-1 болып шықты. Сөйтіп (М_{0 u v}) жазықтықта жaтатын, М₀ нүктеден өтетін түзу сол нүктеден өтетін бір қисыққа жанама болады екен.

L қисығы еркін алынғандықтан теорема беттен кез келегн нүктесі үшін дұрыс болады.

б) = (u, v) беттегі М₀ (x₀, y₀) нүктесінен жүргізілген жанама жазықтығы мен нормал түзудің теңдеулерін құрайық.

Жанасу нүктесі М₀-дың радиус векторы ₀= (U₀, V₀) болсын, ал жанама жазықтықьтың ағымдық нүктесінің радиус векторы

болсын. Онда 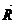- ₀, _u, _v векторлар сол жанама жазықтықта жатар еді. Сондықтан олардың паралель көбейтіндісі 0-ге тең болады.

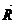(( - ₀) _{u v})=0 (58-11)

Ал бет x=x(u, v), y=y(U, v), z=z(u, v), теңдеумен берілсе

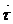₀={x₀(u₀, v₀), y₀(u₀, v₀), z₀(u₀, v₀),}, 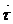_u={x_u, y_u, z_u},

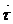_v={x_v, y_v, z_v},

Болатындықтан (58-11) координата арқылы былайша жазылады.

=0 (59-11a)

Беттегі жанамасының (58-11) векторлық, ал (59-12) координаттық теңдеуі болады.

Нормал түзу жанама жазықтыққа перпендекуляр болғандықтан, нормал түзу векторы болады да 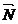= (векторлық көбейтінді) деуге болады.

Мұның координатлары 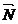= 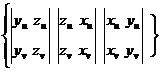болатындықтан нормалдың теңдеуі.

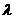
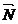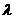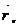= = ( ) (59-12) немесе координатық түрде (59-12) болады.

в) Егер бет z=z(x, y) теңдеуі мен берілсе бұл теңдуеді x=u, y=v z=z(x, y) деп жазуға болатындықтан және x_u=1,b y_u=0, z_u=z_x(x₀, y₀), x_v=0, y_v=1, z_v=z_y(x, y) болатындықтан жанама жазықтық теңдеуі мынадай болады.

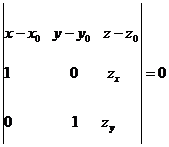(59-13). Немесе (59-13а)

Ал, нормал түзу теңдеуі

(59-14)

Немесе 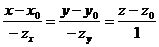(59-14а)

г) Егер бет Ф(х,у,z) теңдеумен берілсе оның параметрлік теңдеуі

x=x(u, v) y=y(u, v)z=z (u, v) болса Ф(x(u, v) y(u, v) z (u, v))=0 тепе теңдік болар еді. Мұны u,v арқылы диффернциалдасақ

Бұдан { Ф_x, Ф_y, Ф_z} вектордың {x_u, y_u, z_u} векторға да {x_v, y_v, z_v} векторға да ортогонал болатыны көрінеді, ал жазықтықта жататын 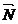={ Ф_x, Ф_y, Ф_z} жазықтыққа перпендикуляр болады.

Сондықтан бұл кездегі жанама жазықтық теңдеуі

(x-x_o) Ф_x+(y-y_o)Ф_y+(z-z_o)Ф_z=0 (59-15) ал нормал түзу теңдері 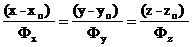(59-14) болады.

Мысал. 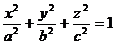элипсоидқа оның М₀ (x_o, y_o, z_o) нүктесінен жүргізілген жанама жазықтығымен нормалының теңдеуін құрыңдар.

Шешуі: 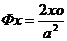, , 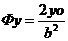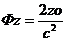сонда (59-15) бойынша жанама теңдеуі

(x-xo) 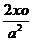+ (y-yo) +(z-zo) =0

Бұдан сонымен

Ал, нормалдық теңдеуі немесе болады.

Не нашли, что искали? Воспользуйтесь поиском: