
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Беттен қисықтар арасындағы бұрыш.
Д облыста u=u1(t), v=v(t) және u=u2(t), v=v2(t) теңдеулермен екі сызық берілсін. Олар Д облысты F бетке көрінетін гомеоморфизмде
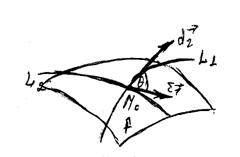
М0(uo, vo) нүктеде қиылысатын L1, L2 қиылыстарға көшсін. Бұл қисықтар арасындағы бірінші деп М0 нүктеден оларға жүргізілген жанамалар арасындағы бұрышты айтады (374-сурет). Eгер бұл қисықтар бойымен дифференциалдауды d және 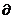 деп белгілесек, онда бұл сызықтарға жүргізілген жанамалар.
деп белгілесек, онда бұл сызықтарға жүргізілген жанамалар.
d  =
=  du+
du+ 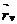 dv,
dv, 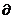
 =
=  δu+
δu+ 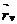 δv бағытта болар еді. (d
δv бағытта болар еді. (d  вектор бағытына
вектор бағытына  мен
мен 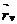 әсер етпейді. Олар М0 нүкте үшін тұрақты болады. Сондықтан d
әсер етпейді. Олар М0 нүкте үшін тұрақты болады. Сондықтан d  бағытты du:dv қатынас анықтайды. Беттегі М нүктенің du:dv бағыты деп d
бағытты du:dv қатынас анықтайды. Беттегі М нүктенің du:dv бағыты деп d  =
=  du+
du+ 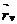 dv вектор бағытын айтады). d
dv вектор бағытын айтады). d  мен
мен 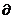
 жанама векторлары арасындағы бірінші Ө болсын.
жанама векторлары арасындағы бірінші Ө болсын.
Сонда
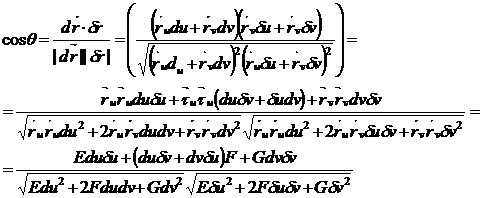
Сонымен L1, L2 қисықтар арасындағы Ө бұрыш мына формуламен табылады.
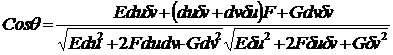 (60-6)
(60-6)
u сызығы бойынша v=Const, v -сызығы бойында u=const болатындықтан dv=0, δu=0 болады да u мен v сызықтар арасындағы бұрыш
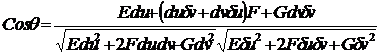
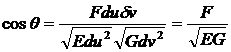 (60-7) формуламен табылады.
(60-7) формуламен табылады.
Егер координаттық тор ортогонал болса, яғни Ө=900 болса, онда
cosӨ =cos90o болатындықтан (60-7) ден F=0 болады. Сөйтіп F=0 болатын беттер үшін координаттық тор дара ортогонал болады.
Беттегі қисықтар арасындағы бұрышты өзгертпей бетті түрлендіру конформды түрлендіру делінеді. Географиялық крталар жер бетін конформды кескіндеу болып табылады.
60.4 Бет ауданы F мынадай үш шартқа бағынатын бет болсын: 1-ол қандайда бір жатық беттің бөлігі болсын, 2-ол тұйық дөңгелекке гомеморфты болсын 3 - F тің жиегі үздікті жатық сызық болсын.
Мұндай беттердің ауданының болатындығы математикалық талдау курсында дәлелденеді. Ауданы болатын бетті квадратталынатын бет деп атайды.






 F квадратталынатын бет болсын,
F квадратталынатын бет болсын,  =
=  (u,v) оның векторлық теңдеуі болсын. (375 сурет) Ол бетті u, v сызықтары координаттық тоорға жіктейді. Сол тордың бірі MM1M3M2 қисық сызықты паралелограмм болсын. Ол 345-б суретте v v
(u,v) оның векторлық теңдеуі болсын. (375 сурет) Ол бетті u, v сызықтары координаттық тоорға жіктейді. Сол тордың бірі MM1M3M2 қисық сызықты паралелограмм болсын. Ол 345-б суретте v v
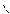


 N2 N3
N2 N3
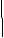
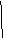
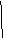







 m2 n2 u M3
m2 n2 u M3



 m m1 u
m m1 u


 M M1
M M1
а) б)
374-сурет
жеке сызылған М нүкте (u,v) параметр сай келсін. Ол нүктенің радиус векторы 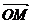 =
=  (u, v) болсын. Нүкте u сызығы бойымен қозғалып Δu өсімше алып M мен M, нүктеге келсін, V сызығы бойымен қозғалып Δv өсімше алып М2 нүктеге барсын. Сонда қисық сызықты паралелограмм төбелерінің координаталары M(u,v), M1(u+Δu, v), M2(u, v+Δ v), M3(u+Δu, v+Δv) болар еді осы кездегі радиус вектор өсімшені.
(u, v) болсын. Нүкте u сызығы бойымен қозғалып Δu өсімше алып M мен M, нүктеге келсін, V сызығы бойымен қозғалып Δv өсімше алып М2 нүктеге барсын. Сонда қисық сызықты паралелограмм төбелерінің координаталары M(u,v), M1(u+Δu, v), M2(u, v+Δ v), M3(u+Δu, v+Δv) болар еді осы кездегі радиус вектор өсімшені.
MM1=  (u+Δu, V)-
(u+Δu, V)-  (u, v),
(u, v),  =
=  (u,v+Δv)-
(u,v+Δv)-  (u, v).
(u, v).
болады. Бұл қисық сызықты өсімшелерді түзу сызықты дербес дифференциалдармен, яғни MM1, MM2 - лерді  uΔu,
uΔu,  vΔv - лармен алмастырайық.
vΔv - лармен алмастырайық.
Сонда MM1M2M3 қима сызықты паралелограмм бетке M нүктеде жанасатын жазықтықта жатқан түзу сызықты MN1N2N3 паралелограммға айналады.
Ол паралелограмның ΔS десек
ΔS=|  uΔu
uΔu 
 vΔv|=|
vΔv|=|  u
u 
 v| ΔuΔv болар еді. Сонда F беттегі барлық паралелограмм аудандарының қосындысы.
v| ΔuΔv болар еді. Сонда F беттегі барлық паралелограмм аудандарының қосындысы.  болар еді.
болар еді.
Ал, |  u
u 
 v|=|
v|=|  u||
u||  v| sin (
v| sin ( u^
u^  v),
v),  u·
u·  v=|
v=|  u||
u||  v|cos(
v|cos( u^
u^  v) болатындықтан, бұларды квадраттап қоссақ |
v) болатындықтан, бұларды квадраттап қоссақ |  ux
ux  v|2+|
v|2+|  u
u  v|2 = |
v|2 = |  u|2|
u|2|  v|2 болады.
v|2 болады.
Бұдан |  u
u 
 v|=|
v|=|  u|2|
u|2|  v|2 - |
v|2 - |  u
u  v|2 =EG-F2 сонымен |
v|2 =EG-F2 сонымен |  u
u 
 v|2 = EG-F2
v|2 = EG-F2
|  u
u 
 v|=
v|= 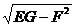 (60-8).
(60-8).
Егер(*) дан Δu мен Δv ны 0-ге ұмтылдырып шекке көшсек 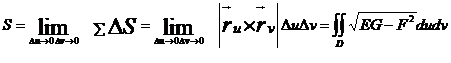 шығады.
шығады.
Сонымен бет ауданы 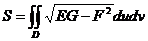 (60-9) формуламен анықталады. Демек беттегі облыс ауданын табу үшінде ол беттегі бірінші квадрат формасын тапса жеткілікті болады екен.
(60-9) формуламен анықталады. Демек беттегі облыс ауданын табу үшінде ол беттегі бірінші квадрат формасын тапса жеткілікті болады екен.
Мұндағы Д қарастырып отырған F бетке сәйкес келетін u мен v ның өзгеру облысы (яғни Д топологиялық бейнесі F болатын жазық облыс(.
Егер бет z=f(x,y) теңдеумен берілсе E=1+fx2, F=fxfy, G=1+fy2 болатындықтан (60.1-де айтылған) бұл беттегі облыс ауданы.
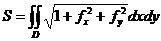 (60-10) болады деген.
(60-10) болады деген.
Бұл кезде Д деген F беттен Оху жазықтықтағы проекциясы х,у сол облыста өзгеруі керек.
Не нашли, что искали? Воспользуйтесь поиском: