Беттің екінші квадраттық формасы.

С^к -классты (k ≥ 1) элементар жатық F беті = (u, v) (61.1) теңдеумен берілсін. Бұл бетте M(u, v) нүкте және ол нүктеден өтетін u=u(s), v=v(s) (61-2) теңдеуімен анықталатын L жатық қиысығы жатсын. Онда M нүкте бұл қисық бойымен қозғалғанда d = _udu+ _vdv болар еді. Бұдан d² = _uudu²+2 _vvdudv+ _vvdv²+ _ud²u+ _vd²v

Мұндағы 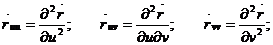екінші дербес туындар

_u, _v векторлар бетке M нүктеде жанасатын жазықтықта жататын. Жазықтыққа осы жанасу нүктесінен жүргізілген түзуді беттен M нүктедегі нормалы дейді. Ол нормалдың бағыты үшін _{u v} векторлық көбейтінді, вектор бағытын алуға болады. (60-8) бойынша | _{u v} |= болатын. Сонда беттің нормалының бірлік векторын десек (376-сурет)

(61-3) болады.

Беттің екінші квадраттық формасы I₂ деп мына век тордың скаляр көбейтіндісін айтады.

I₂=(-d ·d )

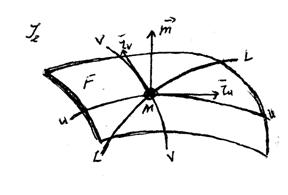
376-сурет

Ал, d болатындықтан d · =0 болады. Бұдан d dm+d² · =0

(-d ·d )=(d² · ) болатындықтан беттің екінші квадраттық формасы (*)-ны -ге көбейту арқылы табылады.

I₂=(-d ·d )=(d² · )=( _uu )du²+2( _uv )dudv+( _vv )dv²+

+( _u )d²u+( _u ) d²v=( _uu ) du²+2( _uv )dudv+( _vv )dv²

Мынадай белгі ендірейік

_uu =L _uv =M, _vv =L; _uv =M _vvm=N

Сонда беттің М нүктедегі екінші квадраттық формасы

J₂=Ldu²+2mdudv+ndv² (61-4)

Егерде (u, v) вектор координаталары {x(u, v), y(u, v), z(u, v) болатын болса, онда _u={x_u, y_u, z_u} _v={x_v, y_v, z_v}, uu={x_uu, y_uu, z_uu}, _uv={x_uv, y_uv, z_uv} vv={x_vv, y_vv, z_vv} болатындықтан беттің екінші квадраттық формасының кэфициенттері былайша анықталар еді.

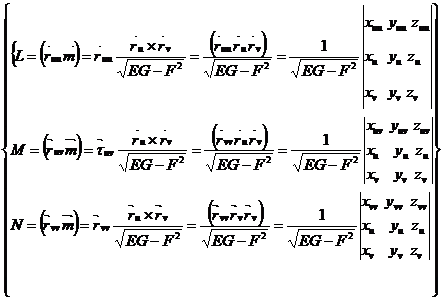
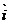Егер бет Z=f(x, y) теңдеумен берілсе, онда =x +y 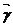+f(x, y) 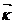болатындықтан x_x=1, y_x=0, z_x=f_x(x, y), x_y=0, y_y=1, z_y=f(x,y) болады да ал E=1+0+f_x²=1+f_x²; F=0+0+f_xf_y=f_xy; G=1+f_y² болып шығады. _x={ 1, 0, f_x }, _y= { 0, 1, f_y } Ал _xx= { 0, 0, f_xx }, _xy= { 0,0,f_xy } _yy= { 0, 0, f_yy }

Сонда бұл кездегі беттегі екінші квадратқа формасының коэфициенттері

;

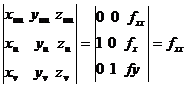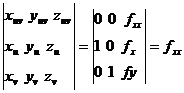
, ал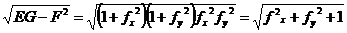

болатындықтан

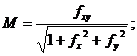
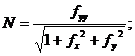
Сонда екінші квадраттық форма

(61-6)

Не нашли, что искали? Воспользуйтесь поиском: