Беттің бас бағыты.

Аналитикалық геометрияда егер 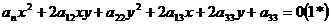теңдеуімен екінші ретті сызық берілсе, онда вектор бұл сызыққа қарағанда 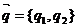векторға түйіндес делінеді. Егерде олар арасында мына шарт орындалса.

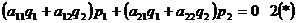
вектор (1*) сызыққа қарағанда басты бағытта делінеді.

Егерде ол өзіне ортогонал 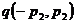векторға осы сызыққа қарағанда түйіндес болатын болса, яғни мына шартты қанағаттандыратын болса (2*) дағы мен алмастырса: деген тұжырымдар дәлелденеді.

Жатық Ғ бет 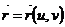(61-1) теңдеуі мен берілсін. Оның M нүктедегі индикатриасы 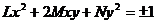(61-8) болсын.

Беттің М нүктедегі Дюпен индикатрисасының бос бағыты (яғни қисықтың индикатрисасының бос остерінің бағыты) беттің осы нүктедегі бас бағыттары делінеді.

Беттің M нүктедегі басты бағыттары 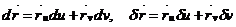векторлармен анықталсын.

Онда олар 1-ден ортогонал 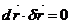боу керек ал, 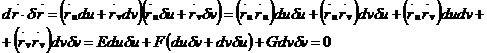(61-9)

2-ден индикатриса сызығына қарағанда түйіндес болуы керек. Яғни (2*) шартын қанағаттандыруы керек.

Бізде 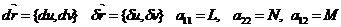болғандықтан түйіндестік шарт (2*) бойынша болу керек. Бұдан (61-10). Бұл шартты былайша да жазуға болады.

(61-11)

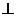
Мұндағы беттің нормалына бірлік векторы шынында да _u болатындықтан .

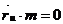Бұдан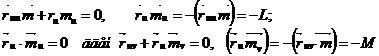

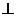
_u болатындықтан · _v=0 бұдан _vu + _{v v}=0 және 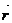_vv + _{v v}=0 бұлардaн ( _v u)=-( _vu )=-M; _{v v}=-( _{v v})=-N

Ал, d ·δ =( udu+ vdv)( _u δu+ _v δv)= ( _u u) du δu+( _u v)dv δu+( _v u)du δv+( v v)dv δv=-Ldu δu-Mdv δu-Mdu δv-Ndvδv=

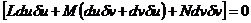= немесе Lduδu+M(duδv+dvδu)+Ndvδv=0. Ал, бұл бағыттың түйінденс болу шарты (61-9) – бен дәлелдер келеді.

Сондықтан түйіндестік шарты d ·δ =0 деп жазуға болады.

Сөйтіп d , δ бағыттар бетінің бас бағыттары болу үшін d ·δ =0, d δ =0 (61-12) болулары керек екен.

Родриг теоремасы

Родриг (Б.О. Родригес 1794-1851) – француз математигі. Теорема былайша тұжырымдалады. d вектор (61-1) теңдеумен берілген беттің М нүктедегі басты бағыты болу үшін d =-kd (61-13) болуы қажетті және жеткілікті. Мұндағы беттің М нүктедегі нормалының бірлік векторы ал K – вектор d бағытындағы нормал қисық.

Дәлелі d = _udu+ _vdv M нүктедегі бірінші басты бағытты вектор болсын.

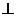
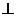
δ = _uδu+ _vδv екінші басты бағыттағы вектор болсын. Онда d ·δ =0 болу керек. Ал мен d = _udu+ _vdv перпендикуляр болатындықтан _u, _v болады. Сондықтан d жанама жазықтықта жатады.

Ал, d ·d =0 болғандықтан, олар коллинор болады. Яғни 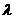d = d 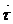болатын 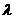саны табылады. Енді 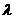=-k болатынын дәлелдейік.

Ол үшін d = 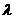d - ден бұдан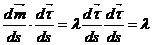

Өйткені бірлік вектор сонымен

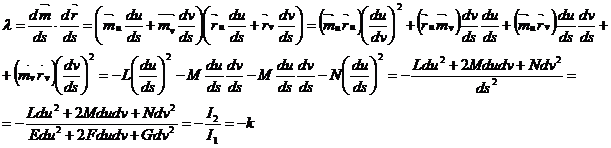
Сөйтіп 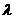=-k, d = 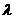d =-kd болады екен.

Керісінше d =-kd болсын. d -дің бос бағытты анықтайтынына көз жеткізейік.

d -ге ортогонал бағытты алайық, онда δ d =0 болады. Ал d =-kd болғандықтан d δ =(-k d )d =k(d δ )=0.

Сөйтіп (61-11) орындалады. Сондықтан d басты бағыт болады. Теорема дәлелденді.

(61-13) формула d =-kd Родригес формуласы делінеді. М нүктедегі басты бағыттағы нормал қисықтың беттегі осы нүктедегі бас қисықтығы дейді.

Родригес формуласындағы К беттен M нүктедегі d 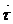бaс бағыттағы бос қисықтығы болады.

Егер Родригес формуласын толық жазсақ _udu+ _vdv=-k( _udu+ _vdv)

Мұны u мен v- ға көбейтсек

( _{u u})du+( _vu)dv=-k[( _{u u})du+( _{v u})]dv

( _{u v})du+( _v v)dv=-k[( _{u v})du+ ( _{v v})]dv

Орындарына қойсақ 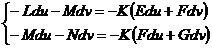4(*)

Бұдан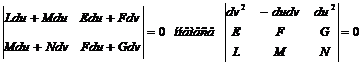

Мұның алғашқысынан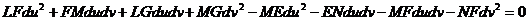

(61-14)

Міне осы формула беттің берілген нүктедегі бас бағыты du:dv табылады.

Ескерту 1. Ғ қарапайым бет болса, онда ол жазықтықта жатады. Ол жазықтық нормалы тұрақты болады. Сондықтан _u, _v нөдік вектор болады да L=M=N=0 болады. Демек мұндай бет үшін кезкелген бағыт бас бағыт болады. Яғни бас бағыт анықталмаған болады.

Ескерту 2. беттегі қисықтың әрбір нүктесіндегі жанама басты бағытта болса, ол сызықты қисықтың сызығы дейді.

Беттің координаттық тор сызықтағы К -сызығы мен V- сызығы қисықтық сызықтары болса, онда беттің әрбір нүктесінде Ғ=0, М=0 болады.

Сондықтан мұндай беттің нүктелеріндегі 1-2 квадраттық формалар

(61-15) болады.

Не нашли, что искали? Воспользуйтесь поиском: