
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Беттегі қисықтың қисықтығы
Ғ жатық бетті (61-1) теңдеуімен, онда жатқан қисық табиғи параметр арқылы (61-2) теңдеумен берілсін. Онда ол сызықтың векторлық теңдеуі  =
=  =(u(S), v(S)) болар еді.
=(u(S), v(S)) болар еді.
Бұдан алынған 1-туынды қисыққа М нүктедегі жанама вектор болады.  =
=  u
u 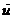 +
+  v
v  мұндағы
мұндағы  =
=  u
u 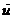 +
+  v
v  арқылы белгілейміз (өйткені -
арқылы белгілейміз (өйткені -  =
=  бірлік вектор болатын).
бірлік вектор болатын).
Бұдан алынған  туындыны қисықтың қисықтық векторы дегеніміз:
туындыны қисықтың қисықтық векторы дегеніміз:
 =
=  uu
uu 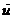 2+
2+  uv
uv 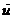
 +
+  uu
uu 
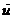 +
+  u
u 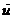 +
+  vv
vv  2+
2+  v
v  2
2
Мұның ұзындығын |  |=k қисықтың берілген нүктедегі қисықтығы деген едік. Ол Френенің екінші формуласы бойынша қисықтың бос нормаларының
|=k қисықтың берілген нүктедегі қисықтығы деген едік. Ол Френенің екінші формуласы бойынша қисықтың бос нормаларының
бірлік векторы 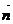 мен былайша байланысатын
мен былайша байланысатын  =k
=k 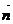 . Егер L сызықтың M нүктедегі бас нормалы
. Егер L сызықтың M нүктедегі бас нормалы 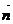 -шы беттің M нүктедегі нормалы
-шы беттің M нүктедегі нормалы  аралығындағы бұрышты Ө десек онда |
аралығындағы бұрышты Ө десек онда | 
 |=k(
|=k(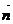
 )=k|
)=k| 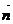 ||
||  | cosӨ = k·1·1cosӨ=kcosӨ болады.
| cosӨ = k·1·1cosӨ=kcosӨ болады.

377-сурет
Бұл қисықтың векторы  -нің сол нүктеден жүргізілген бет нормалы
-нің сол нүктеден жүргізілген бет нормалы  -ге түскен проекциясы болады. (377-сурет) k(
-ге түскен проекциясы болады. (377-сурет) k(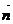
 )=ku деп белгілеп L қисықтық M нүктедегі нормал қисықтығы дейді. Екінші жағынан
)=ku деп белгілеп L қисықтық M нүктедегі нормал қисықтығы дейді. Екінші жағынан
(
 )=(
)=( uu
uu  )
) 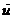 2+(
2+( uv
uv  )
) 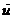
 +(
+( vu ·
vu ·  )
) 
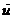 +(
+( u ·
u ·  )
) 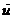 +(
+( vv
vv  )
)  +(
+(
 )
)  2=
2= 

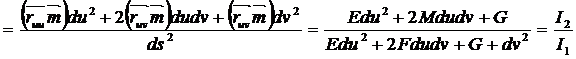
Сонымен соңғы екі теңдіктен  тұрақты сонда
тұрақты сонда  (61-7)
(61-7)
Kn -нің шамасы беттегі L қисықтың нүктедегі нормал қисықтығы ал к нүктедегі сол нүктедегі қисықтығы болады. (61-7) теңдеуі Менье теоремасы деп аталады.
Егерде L, беттің нормал қимасы болса (яғни беттегі M нүктеден жүргізілген нормалын басып өтетін жазықтықты беттің қимасы болса (онда  мен
мен 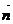 бағытта (
бағытта ( ↑↑
↑↑ 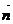 ) не қарама – қарсы бағытта (
) не қарама – қарсы бағытта ( ↑↓
↑↓ 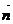 ) болатыны түсінікті (мәні Ө не 00 не 1800 болады).
) болатыны түсінікті (мәні Ө не 00 не 1800 болады).
Бірінші жағдайда жағдайда  , екінші жағдайда
, екінші жағдайда  болады.
болады.
Сөйтіп нормал қиманың нормал қисықтығы абсалют жанама жағынан қиысатын сол нүктедегі қисықтығына тең болады.
Егер  бағытта
бағытта 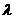 десек
десек  онда деуге болады.
онда деуге болады.
Бұдан беттегі қисықтың M нүктедегі нормал қисықтығы сол нүктедегі жанама бағытына ғана байланысты болатын көрінеді. Сондықтан беттің бір нүктесінен өтетін және бір ортақ барлық жанамамен қисықтардың нормал қисықтары бірдей болады.
Демек беттің M нүктесінен өтетін кез келген қисықтың нормал қисықтығы сол қисықпен ортақ жанамасы нормал қиманың қисықтығына абсалют ашама жакғынан тең болады.
Не нашли, что искали? Воспользуйтесь поиском: