Беттің бас,орташа. Толық қисықтары

(4-*) дан бұдан

(61-16)

Осы квадрат теңдеуден беттегі бас қисықтығы К₁, К₂ табылады.

Вист теорема бойынша

Бас қисықтардың жарты қосындысы беттің М нүктедегі орташа қисықтығы, ал олардың көбейтіндісі К₁ К₂ беттің М беттің нүктедегі толық қисықтығы немесе Гаустық қисықтығы делінеді

К_r = К₁·К₂ сонымен беттің орташа қисықтығы

(61-17)

Беттің толысу (Гаустың) қисықтығы формуласымен табылады.

EG-F²=| _{u v}| болатындықтан EG-F² > 0. Сонықтан элипстік нүктеде 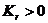гиперболаның нүктеде параболалық нүктесі болады. Егер Ғ қарапайы бет болса, 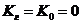болды.

Эйлер формуласы

Енді беттің М нүктедегі еркін бағыттағы нормал қисықтығы мен сол нүктеден басты нормал қисықтар арасындағы байланысты анықтайық. Ол үшін беттің M нүктесінен өтетін координаттық сызықтарын _u мен _v басты бағытта болатындай етіп алайық. Онда _{u 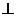v} болады. Сондықтан F=0, M=0 болады. Бұл кезде M нүктедегі нормал қисықтың (61-7а) бойынша

(5*)

Нормал қима L- дің M нүктедегі жанамасының бірлік векторын дейін ол _u мен нүктедегі бұрыш жасасын ( _u мен _v ол нүктедегі басты бағыттар)

_v

t

M _u

(379-сурет).

(379-сурет) Сонда L сызық бойымен қозғалғанда

Мұны _u мен _v кезең – кезең көбейтсек

Сонымен

Бұлардан

Мұны (5*) – ке қойсақ

(68-18)

Егер =0 болса, онда жанама мен _u беттесер еді, (61-18) – ден (61-19), ал = болсa, 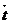мен _v беттеседі де (61-20).

Бұлардан (61-21)

Мұндағы К₁ -бірінші басты бағыттағы басты қисықтың, К₂ - екінші басты бағыттағы басты қисықтың, ал К_n вектор бағыттағы нормал қисықтық. Бұлар өзара (61-21) формуламен байланысады. Оны Эйлер формуласы деп атайды. ол басты бағытпен бұрыш жасайтын бағыттағы нормал қисықтықпен осы нүктедегі бас қисықтықтарды байланыстырады.

Эйлер формуласын былай жазамыз.

бұдан болса, мысалы болса онда K_n max мәнге ие болу үшін =0 не =180⁰ болу керек. Бұл _u осьтің бағыты. Бұл кезде K=K₁ K_nmin мәнге ие болу үшін =90⁰ не =270⁰ болу керек. Бұл _v бағыты. Бұл кезде k₁=k₂. Бұдан берілген нүктедегі басты бағыт сол нүктедегі нормал қисықтың экстремум мәнге ие болатын бағыт екені көрінеді. Егер K₁=K₂ болса K_n=K₁ cos² +k₁sin² = k₁=k₂ боладыда нүктедегі барлық бағыт басты бағыт болады.

Не нашли, что искали? Воспользуйтесь поиском: