
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Деривациялық формулалар.
(Дериват латнша derivayus- қандайда бір алғашқы нәрсенің туындысы, алғашқы нәрселерден туындайтын нәрселер деген ұғымды білдіреді.
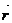 =
= 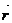 (u,v) теңдеумен бет берілсін. Бетте M(u,v) нүкте жатсын. Бұл нүктеден өтетін координаттық u,v сызықтардың жанамалары
(u,v) теңдеумен бет берілсін. Бетте M(u,v) нүкте жатсын. Бұл нүктеден өтетін координаттық u,v сызықтардың жанамалары 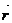 u,
u, 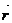 v ол беттің нормалының бірлік векторы
v ол беттің нормалының бірлік векторы  болсын. Онда
болсын. Онда  u,
u, 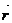 v
v  компланар болмайды және ол үштік жасайды. Сондықтан бұларды беттің М нүктесінен жүргізілген репер (координата жүйесі) деп қарасытруға болады. Оны R=(
компланар болмайды және ол үштік жасайды. Сондықтан бұларды беттің М нүктесінен жүргізілген репер (координата жүйесі) деп қарасытруға болады. Оны R=(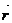 u,
u, 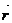 v
v  ) деп белгілейік.
) деп белгілейік.
Сонда кезкелген векторд, оның ішінде 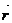 uu,
uu, 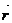 uv,
uv, 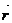 vv,
vv,  u,
u,  v векторларды да R базиске бір мәнді жіктеуге болады. Олар былай жіктелсін.
v векторларды да R базиске бір мәнді жіктеуге болады. Олар былай жіктелсін.
 (62-1,2,3,4,5)
(62-1,2,3,4,5)
Мақсат осы жіктелу коэффициенттерін 1-2 квадраттық форма коэфициенттері және олардың u,v арқылы алынған туындылары арқылы табу.
m -бірлік вектор болғандықтан 
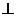
 u,
u, 
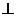
 v, және анықтама бойынша
v, және анықтама бойынша 
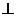
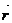 u,
u, 
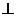
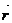 v сондықтан
v сондықтан
 болады. Бұлардан
болады. Бұлардан
 (2)
(2)

Осыларды ескере отырып (62)-і  -ге көбейтсек
-ге көбейтсек

Енді (62-нің әрқайсысын 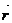 мен
мен 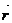 - ға көбейтеміз.
- ға көбейтеміз.

(5)-тің алғашқы екеуінен
 (62-6)
(62-6)
Сөйтіп (62-1,2,3,4,5)-дегі барлық коэффициенттерді таптық.
Бұл (6)формуладағы (61)-ге қойғаннан кейін өрнекті диривациялық формулалар дейді., ал  коэффициенттерді Кристоффель коэффициенттері немесе екінші текті Кристоффель символы дейді, ал
коэффициенттерді Кристоффель коэффициенттері немесе екінші текті Кристоффель символы дейді, ал  яғни (5)-тің алғашқы жұбының оң жағы Кристофельдің бірінші ретті символдары делінеді. (Кристоффель (1829-1900) неміс математигі).
яғни (5)-тің алғашқы жұбының оң жағы Кристофельдің бірінші ретті символдары делінеді. (Кристоффель (1829-1900) неміс математигі).
Кристофельдің (2-ретті символдары) коэффициенттері тек беттің бірінші квадраттық формасының коэффициенттері және олардан алынған туындылар арқылы өрнектеледі. Сондықтан олар беттің ішкі геометриясының объектілері болады. Демек беттің ішкі геометриясын оқуға оларды қолдануға болады.
62.4 Гаус теоремасы.
Карл Гаус (1777-1855)-неміс математигі, астраномы, геодезист. Ол бетті параметризациялауды, бірініш және екінші квадраттық форманы ендірген. Беттегі қисықтың қисықтығы, бетті ию кезіндегі қисықтықтың сақталуы, геодезиялық үшбұрыш бұрыштарының қосындысы жайлы теорема.
теорема Ck классты жатық беттің толық қисықтығы тек беттің бірінші квадраттық формасының коэффициенттері және оның туындылары арқылы өрнектеледі.
Дәлелі: Бет  =
=  (u, v) теңдеумен берілсін беттің толық қисықтығы
(u, v) теңдеумен берілсін беттің толық қисықтығы  формуласымен анықталатын мынадай еді.
формуласымен анықталатын мынадай еді.

Бұдан 
|
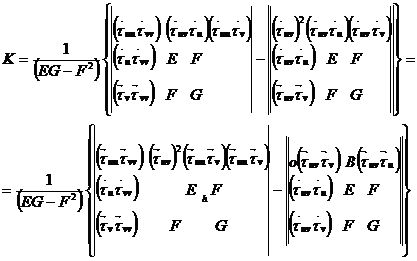
Мұндағы 
Мұның екіншісімен
Төртіншінен 
 uuv=
uuv=  uvu,
uvu,  uv=
uv=  vu болатын (себебі олар үздіксіз функциялар) ескеріп бір-бірімен шекерсек
vu болатын (себебі олар үздіксіз функциялар) ескеріп бір-бірімен шекерсек
( uu
uu  vv)-(
vv)-( uv)2=Fuv-
uv)2=Fuv- 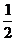 Guu-
Guu- 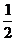 Evv
Evv
Бұларды орындарына қойсақ

Сонымен теорема дәлелденді. Шынындыда жатық беттегі Толық (Гаустық) қисықтығы беттің бірінші квадраттық формасының коэффициенттері және олрдан u, v арқылы алынған туындылар мен толық анықталады екен. Сондықтан ол беттің ішкі геометриясының объектісі болады.
Не нашли, что искали? Воспользуйтесь поиском: