Беттегі қисықтың геодезиялық қисықтығы

С^к классты бет = (u,v) теңдеумен, ал ол бетте жатқан L сызығы табиғи параметр арқылы u=u(s), v=v(s) теңдеумен берілсін. беттің М нүктесінен (ол нүктеден L қисықта өтсін) бетке жанама жазықтық жүргізейік -осы М нүктедегі бет нормалының бірлік векторы. берілген L сызығына М нүктедегі жүргізілген жанаманың бірлік векторы, сол сызықтық

0 L

k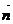

381-сурет

М нүктедегі қисықтың векторы болсын (ол L сызықтың ойыс жағына қарай бағытталады, өйткені 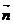солай бағытталады), 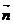вектор L қисықтың М нүктедегі бас нормалының бірлік векторы (381-сурет) К сызықтың М нүктеден қисықтығы болсын.

дан Френс формуласы бойынша

еді.

Бұған деривациялық формуланы пайдалансақ

Мұны _u, _v, арқылы топтасақ.

U нүктедегі сызықтың қисықтық векторы екі векторға жіктеледі екен. (62-12)

(62-13)

(62-14)

Мұның 1-сі _u мен _v жатқан жанама жазықтықта жатса, екіншісі бет нормалы -ге коллинар болады. Сондықтан қисық жанамасы -ға М нүктеде ортогонал болады.

-вектор беттегі L қисықтың М нүктесіндегі геодезиялық қисықтың векторы делінеді.

(62-12) ден болғандықтан болады. Ал , болғандықтан векторы векторлардың векторлық көбейтіндісіне коллинар болады.

Сонда десек (62-15)

Мұндағы санын L қисықтың М нүктедегі геодезиялық қисықтығы дейді бірлік вектор болғандықтан |Kg|=| | (62-15а).

Сөйтіп геодезиялық қисықтық вектордың ұзындығын сол нүктедегі қисықтың геодезиялық қисықтығы дейді екенбіз.

(652-13) – тің Кристоффель коэффициенттері беттің бірінші квадраттық формасының коэфициенттері және одан алынған туындылар арқылы өрнектелетін қисықтың геодезиялық қисықтығы да беттіңбірінші квадраттық формасының коэффициенттері мен олардың туындылары арқылы өрнектеледі. Сондықтан ол беттің ішкі геометриясы қарастыратын мәселелерге жатды.

(62-14) – тің коэффициенті.

болтындықтан L қисқтың М нүктедегі норма қисықтығын білдіреді.

Сондықтан

Сөйтіп (62-16)

(62-15, 16) – дан Бұдан егер десек менбе теоремасы бойынша екенін ескерсек

Сонымен (62-17)

Мұнымен формуладан

Сөйтіп (62-18)

Осы формуламен қисықтың М нүктедегі бас қисықтығы нормал қисықтығы геодезиялы қисықтығы байланысады.

(62-15,15а) дан дан .

Бұдан болатынын ескеріп, көрсетілген векторлық көбейтуді орындасақ геодезиялық қисықты табу формуласын аламыз.

62.7 Геодезиялық сызық.

Бетте жатқан сзықтың әрбір нүктесіндегі геодезиялық қисықтығы 0-ге тең болмса онда ол сызықты геодезиялық сызық дейді.

Жатық бет = (u, v) теңдеумен онда жатқан сызық u=u(s), v=v(s) теңдеуімен берілсін.

(62-16) екенін және

(62-17) екенін көрді.

Бұлардан геодезиялық сызық жайлы мынадай тұжырымдар жасауға болады.

1^о (62-17) ден K_g=0 болу үшін не K=0, не sinӨ=0 болуы керек.

1-а болсын. Онда біріншісін 0^о не 180^о болады. Яғни болады.

Демек геодезиялық сызықтың әрбір нүктесіндегі қисықтың векторы мен бет нормалы кллинар болады.

1-б Сфераның үлкен дөңгелектерінің бас нормалы центрден беттің сол нүктдегі нормалы мен беттің . Демек сфераның ү лкен диаметрі геодезиялық сызық болады.

1-в қисықтың жанасу жазықтығы бас нормал мен жанама вектор t арқылы өтетін. Олай болса геодезиялық сызықтың әр нүктесіндегі жанасу жазықтығы сол нүктедегі бет нормалынан өтеді екен.

2⁰ Егер k=0, sin Ө≠0 болса, онда беттегі L сызығы түзу болады. (түзу деп әр нүктесінде бас қисық k=0 болады) Демек бетте түзу жатса, онда ол түзу сол бет үшін геодезиялқ сызық болады.

2-б Екі беттің қиылысу сызығы ол беттердің біреуі үшін геодезиялық сызық болады.

Шынынды да қисықтың геодезиялық қисықтығы қисықтық векторының жанама жазықтықтағы проекциясы болады. (62-12) ден десек шығады). Ал, L сызығы бойында жанама жазықтықекі бетке бірдей болады.

3⁰ С^к класты жатық беттің әрбір нүктесінен кезкелген бағытта геодезиялық сызық жүргізуге болады, және ол біреу ақ болады.

(Мұны геодезиялық сызықтың болуы туралы теорема дейді).

Дәлелі беттегі жатық қисық U=U(S), V=V(S) теңдеумен берілсін.

(62-15) теңдеуден берілген сызық геодезиялық болу үшін болуы керектігі шығады, ал болу үшін оның екі координаты да Ө болуы керек.

Сонда (62-13) тен

(62-13)

Сонымен U(S)₁ V(S) осы теңдеудің шешуі болған жағдайда ғана U=U(S)₁ V=V(S) сызығы геодезиялық сызық болады. Ал, (62-18) U(S)_1, V(S) -ке қарағанда екі ретті дифференциялдық теңдеулер және оның коэфициенттері D облысты үздіксіз функциялар. Сондықтан олардың шешуі болады.

Геодезиялық сызықтың теңдеуін анықтау үшін геодезиялық қисықты табуға арналған (62-19) формуладағы Kg=0 деуіміз керек.

Сонда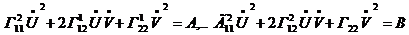

Десек немесе (62-19)

Бұларды геодезиялық сызықтың дифференциялдық теңдеуі дейді. Бұл теңдеуден геодезиялық сызықтың беттің ішкі геометриясының объектісі екені көрінеді.

Ескерту: екі беттегі тордың бір сызықтар үйірі геодезиялық сызқтардан, ал екіншісі оған ортогонал сызықтардан тұрса ол жартылай геодезиялық тор делінеді. Егер беттегі U,V координаттық тор жартылай геодезиялық тор болса (u-геодезиялық сызық болса) онда беттің 1-ші квадраттық формасы.

ds²=E(U₂V) du²+G(U,V)dv²

1. Егер М₁, М₂ геодезиялық сызықтың барынша жазық екі нүктесі болса онда М₁, М₂ доға осы нүктелерді қосатын доғалардың ең қысқасы болады.

62.8 Гаусс – Бонне теоремасы. К Гаусс (1777-1855) неміс математигі. П О Бонне (1819-1892) француз математигі.

Теорема. Ғ жатық бет, Ғ₀ онда жатқан клетка болсын. Клетка шеkарасы жатық сызықтардан тұрсын, ол сызықтар өзара бұрыштар жасасын, онда мына теңдік орындалады.

(62-20)

Теорема дәлелсіз алынады (382-сурет)

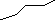
α_i

F Fo

382-сурет

Мұндағы К_g клетка шекаралры сызықтардың геодезиялық қисықтығы К – беттің толық қисықтығы ds- шекаралық доғалар ұзындығының dδ= бет ауданының элементі.

Теорема салдары:

1⁰ Егер Ғ₀ клетка шекарасы бір ғана жатық сызықтан тұрса, онда болады да (62-20) мына түрде болады

(62-20а)

2⁰ Егер сызықтардың барлығы гиперболалық сызықтар болса, онда Ғ₀ тұйық клетка геодезиялық көпбұрыш делінеді.

Бұл кезде барллық сызықтар үшін К_g= 0 болады да (62-20) мына түрге келеді.

(62-20б)

3⁰ егер Ғ жазықтық болса Ғ₀ кәдімгі көпбұрыш болады. деген бұрыштың сыртқы бұрышы болады және k=0 болады.

Сонда (62-20) мына түрге келді.

(62-20в)

Яғни көпбұрыштың сыртқы бұрыштарының қосындысы 2π болады.

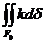шамасын F₀ облысының интегралдық қисықтығы дейді ол белгілі тұрғыда беттің ішкі геометриясының евклидтік жазықтықтағы геометриядан ауытқу дәрежесін сипаттайды.

62.9. Геодезиялық үшбұрыштың дефектісі.

Егер беттегі Ғ₀ клетканың шекарасы үш геодезиялық доғадан тұрса, онда ло клетканы геодезиялық үшбұрыш дейді.

Теорема: Егер геодезиялық үшбұрыштың барлық нүктелеріндегі толық қисықтық К бір таңбасы болса не 0 болса онда ол үшбұрыштың бұрыштарының қосындысы.

a) К>0 болған жағдайда -ден көп болады.

б) К<0 болған жағдайда -ден кем болады.

в) К=0 болған жағдайда -ге тең болады.

Сөйтіп >< - болады

Ғ₀ Ғ геодезиялық үшбұрыш, оның шекаралары геодезиялық сызықтан тұрсын, бұрыштары болсын. Сонда n=3 Kg=0 болғандықтан (62-20) мына түрге келеді.

- бұдан = +

Егер геодезиялық үшбұрыштың әрбір нүктесінде k > 0 болса, онда >0 болады да > болады.

Егер геодезиялық сызықтың әрбір нүктесінде k < 0 болса <0 болады. Ал k=0 болса болады да (62 ге) формуладан < немесе, =0 болып шығады.

Мына сан = геодезиялық F үшбұрыштың дефектісі делінеді. Сонда (62-21) ден

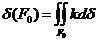(62-22)

Егер F сфера болса

K= 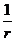(r- сфера радиюсы) болады да сфералық үшбұрыш үшін (62-2) бойынша оның дефктісі.

Мұндағы S(Ғ₀) сфералық үшбұрыш ауданы.

Бұдан S(F₀)=-r² немесе S(F₀)=r² (62-33)

Мұндағы = - бұл сфералық үш бұрыштың бұрыштарының қосындысы π ден артық болады, ал сфераның үшбұрыш ауданы оның «артатынына» пропорционал болады.

Егер Ғ пcевдосфера болса, онда оның толық қисықтығы K= болатын. Сонда (62-22) бойынша певдосфера жатқан геодезиялық Ғ₀ үшбұрыштың дефектісі

мұндағы S(Ғ₀) Ғ₀ үшбұрыш ауданы. Сонымен S(Ғ₀)=+a² (62-24)

Сонымен певдосфералық беттегі геодезиялық үшбұрыштың дефектісі (Ғ₀)= >0 оң болады, яғни үшбұрыш ішкі бұрыштың қосындысы π ден аз болады екен. Ал, бұл певдосфералық беттің кіші аймағында Лабачиекиидің планиметриясы орындалады деген сөз.

2-ден псевдосферадағы үшбұрыш ауданы оның дефектісіне пропорционал болады екен.

Не нашли, что искали? Воспользуйтесь поиском: