Бағдарланатын тұйық жатық беттің эйлер характеристикасы.

Ғ деген Р тұтқалы сфераға гомеморфты жатық бет болсын. Онда ол бағдарланатын көпбейнелік болады.

Теорема:Егер жатық бет Р тұтқалы сфераға гомеморфты болса онда оның эйлер характеристикасы

(62-24)

Формуламен өрнектеледі. Мұндағы К толық қисықтық бет ауданының элементі.

Дәлелі: Ғ клеткаларға жіктелсін, клеткалардың шекарасын үзікті-жатық сызық (әр қабырға жатық сызық болсын) Ғ_к клеткада ** төбе, сонша қабырға жатық сызық болсын. Оның ішкі бұрыштарын дейік.

Ғ жіктелген клеткалардың төбесінің саны қабырғаларының саны , клетка саны дейік.

Ғ_к клетка үшін Гаусс-Бонне теоремасы бойынша

Осындай теңдікті Ғ жіктелген барлық n клетка үшін жазығы, оларды қоссақ және қосу барысында клетканың әрбір қабырғасы екі реттің бір-біріне қарама-қарсы бағытта қосылатындықтан болатындығын ескерсек

шығады.

Мұның сол жағын былайша жазуға болады.

Әр клеткасы деп қабырғаның екі клеткаға ортақ болатындықтан

(әрбір қабырға екі реттен салынған)

Мына қосынды барлық клетка бұрыштарының қосындысы.

Әр төбедегі ішкі бұрыштар қосындысы 2π болатындықтан бұл қосынды 2πα,- 2πα₀ болады.

Сонымен (*) теңдік былайша жазылады:

формула. Бұл (62.24)

Мұның оң жағы Ғ -ті клеткаға болу саны мен тәртібіне тәуелді емес.

Демек Р тұтқалы сфераға гомеморфты болатын жатық беттің эйлер характеристикасы клеткаға болуға тәуелді емес.

Бұл теореманы r радиюсты сфераға пайдaлансақ ( болатындықтан) (62-14) мына түрге келеді.

Сөйтіп сфераның эйлер характеристикасы 2-ге тең болатындығын тағы да дәлелдейік.

Мысал есептер.

1-есеп. Тік геликолд x=u cos γ, y=u sin γ, z=av(o ≤ u <, - ∞ < v < ∞, a≠0) берілген. Ол туралы төмендегі сұрақтардың жауабын анықтаңдар.

Тік геликолд деп бір түзуге (оны геликолд осі дейді) перпенекуляр түзудің ості айнла бірқалыпты және бұрылу бұрышына пропорционал болып оске паралель бағытта қозғалуынан пайда болатын бетті айтады. Оның383 суреттегідей болады.

1⁰ екінші квадраттық формасы қандац болады. 1-ден 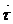={u cos γ, u sin γ, av}, 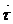_u={cos γ, sinγ, 0} 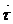_v= {u sin v, cos γ, 0}, 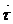_uv={-ucosγ, -usinv, 0}. Бұлардан E= 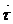_{u 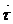u}=cos²γ+sin²γ0=1. 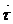_{u 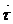v}=-ucosγ sinγ+usinγ cosγ+0=0

G= 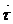_{v 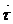v}=u²cos²γ+u²sin²γ+a²=a²+u²

Сонымен беттің 1-квадраттық формасы J¹=Edu²+2Fdu dv+Gdv² =du²+()dv²

2-квадраттық форма болады. J₂=Ldu²+2mdudv+Ndv²= -

2⁰. Бас бағыты менбос қисықтарын орта жіне толық қисықтарын табу керек.

Бас бағыт du:dv мына фромулалармен табылады.

Біздің мысалда LF=0-0=0; ME=- ; LG=0, EN=0; MG=-a MF=0

Сонда -

Бұдан du=±(a²+u²)dv

Немесе dv =±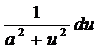

Беттің бас толық, орта қисықтары мына формуладан табылады.

(EG-F²)К_Б²+(2MF-EN-LG)K(LN-M²)=0

Теңдеудің шешімдеі K₁ мен K₂ беттің бас қисықтары, ал орташа қисығы K=K₁ K₂ толық (гаустық) қисықтығы беріледі.

Біздің мысалда Ea=a²+u² ; F=0 M=0, EN=0, LG=0, LN=0, M=- 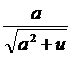орнына қойсақ

Бұдан K_1,2=±

Гаустық қисықтық K=K1 K2=-

Орташа қисықтық

3⁰ беттің М нүктесіндегі бір басты бағытпен 30⁰ бұрыш жасайтын бағыттағы нормал қисықтығын табыңдар.

Бірінші басты бағытпен төрт бұрыш жасайтын бағыттағы беттің нормал қисығы Эйлер формуласымен анықталады.

K_n=K₁cos²φ+K₂hn² φ

Бізде К₁,К₂ белгілі, φ=30⁰ сонда іздеген нормал қисықтық

болады.

Не нашли, что искали? Воспользуйтесь поиском: