Дюпен индикатрисасы .

Дюпен (1784-1873) француз математигі. F бетте M нүктесі берілсін. Ол нүктеден шексіз көп бетте жататын қисықтар жүргізуге болады. Ол қисықтардығң кей біреулері ортақ жанамасы болса, кейбіреулерінің жанамалары болса, әртүрлі түзулер болады. Бір нүктеден өтетін әртүрлі жанамалы қисықтардың нормал қисықтарының арасындағы байланысты анықтайық.

Ол үшін беттегі M нүктесінен бетке жанама жазықтық жүргізіп, сол жазықтықтың M центірлі түзулер шоғын қарастырайық. Ол шоқтың әрбір түзуіне М нүктеден бастап, оның екі жағына да 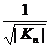кесіндіні өлшеп салайық мұндағы K_n -сол түзу жанамасы болатын қисықтың нормал қисықтығы.

Бұл кесінділердің ұштары жазықтықты бір сызық шығады. Ол сызқты М нүктедегі F беттің қисықтығының индикатрикасы немесе Дюпен индикатрисасы деп атайды.

Дюпен индикатрикасының теңдеуін құру үшін жанама жазықтыққа координаты жүйесін ендірейік. х(х,у) нүкте нүкте индикатрисасының ағымдық нүктесі болсын.

Теңдеуі қисыққа жанаманың бірлік векторы болсын. Онда болар еді. Бұдан болады.

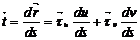Ал, , ал 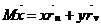болатындықтан .

Бұдан , бұдан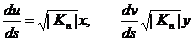

Бұларды (61-7) –ге қойсақ

Болсын 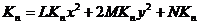немесе (61-8)

Осы қисықтың индикатрисасының теңдеуі болады. Ол екі екінші дәрежелі теңдеуден тұрады екен. Демек қисықтың индикатрисасы екі екінші ретті қисықтан тұрады:

Бұл теңдеуді зерттейік.

1⁰ болсын.

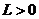деуге болады. Сонда

Бұл L > 0 LN-M² > 0 болғандықтан х,у -тың кезкелген мәнінде оң болады. Ал біз нақты сызықтарды ғана қарастыратындықтан (61-8) де +1ді ғана алуымыз керек екен.

Яғни теңдеуді алуымыз керек екен.

Бұл кезде болғандықтан ∆ инвариант

(шарты бойынша)

Болғандықтан теңдеу элипсті анықтайды. Бұл кезде М нүкте беттің элипстік нүктесі делінеді. Элипсоидтың, екі қуысты гиперболойдтың, элипстік пороболойдтың, барлық нүктелері элипстық нүктелер болады. Егер индикатриса теңдеуі элипс шеңбер болса М нүкте омбликалық нүкте делінеді. Сфера нүктелері омбликалық нүктелерден ғана тұрады.

2⁰ болсын. Бұл кезде индикатриса теңдеуі түйіндес екі гиперболаны анықтайды.

M

(378-сурет)

болғанда оң және сол екі тармақтан, Lx²+2Mxy+Ny²=-1 болғанда үстіңгі және астыңғы екі тармақтан тұратын гиперболаларды анықтайды. (378-сурет) Бұл кезде M нүкте бетінің гиперболалық нүктесі делінеді. Бір қуысты гиперболоид, гиперболалық поролоболоидтар гиперболалық нүктелерден тұрады. Бет M нүктенің аймағында гиперболалық пороболоид түрінде болады.

3⁰ болсын.

Бұл кезде (61-8) дің сол жағы толық квадрат болады сондықтан оң жағы +1 болу керек яғни индикатриса теңдеуі түрде болады. Мұндағы . Бұдан 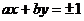болғандықтан индикатриса екі өзара паралель түзу болады. М нүкте беттің параболалық нүктесі делінеді.

Цилиндр төбесі жоқ конус параболалық нүктелерден тұрады.

Не нашли, что искали? Воспользуйтесь поиском: