
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Мысалдар қарастырайық.
1- мысал. 
(0 ≤ u < ∞, 0 ≤ v < 2π) бетте жатқан u= 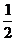 a v2 қисықтық A(u=0, v=0) нүктеден B(u=20, v=2) нүктеге дейінгі ұзындығын табыңдар.
a v2 қисықтық A(u=0, v=0) нүктеден B(u=20, v=2) нүктеге дейінгі ұзындығын табыңдар.
Шешуі: алдымен 1-квадраттық форманы табу керек.
 u={xu, yu, zu}={
u={xu, yu, zu}={ 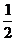 (
( cosv+sinv),
cosv+sinv), 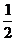 (
( sinv-cosv), 0}
sinv-cosv), 0}
 v={
v={ 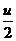 (-
(-  sinv+cosv),
sinv+cosv), 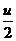 (
( cosv+sinv), a}={xv,yv,zv}
cosv+sinv), a}={xv,yv,zv}
Сонда
E=  u
u  u=
u= 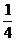 (3cos2v+2
(3cos2v+2  cosvsinv+sin2v)+
cosvsinv+sin2v)+ 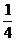 (3sin2v-2
(3sin2v-2  sinv·cosv--cos2v)+02=1
sinv·cosv--cos2v)+02=1
F=  u
u  v=
v=  (-3cosv sinv-
(-3cosv sinv-  sin2v+
sin2v+  cos2v+sinv cosv)+
cos2v+sinv cosv)+  (3sinv cosv –
(3sinv cosv –
-  cos2v+
cos2v+  sin2v-sinvcosv)+0=0
sin2v-sinvcosv)+0=0
G=  v
v  v=
v= 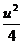 (3sin2γ-2
(3sin2γ-2  sinvcosv+cos2v)+
sinvcosv+cos2v)+ 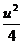 (3cos2 γ+2
(3cos2 γ+2  cos γsin γ+
cos γsin γ+
+sin2 γ)+a2=u2+a2,
Ал, u= 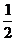 av2 тан
av2 тан 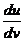 =
= 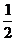 a2v=av
a2v=av
Сонда 
2- мысал. x=ucosv, y=usinv, z=u2 бетттегі v=u+1, v=3-u қисықтар арсындағы бұрышты табыңдар.
Шешуі: xu=cosv, yv=sinv, vu=2u, xv=-usinv, yv=ucosv, zv=0
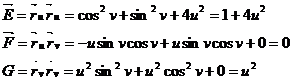
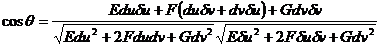
Бізде d белгі v=u+1 бойымен алынған дифференциал dv=du  белгі v=3-u қисығы бойымен алынған дифференциал
белгі v=3-u қисығы бойымен алынған дифференциал
 v=-
v=-  u
u

v=u+1 мен v=3-u сызықтары u=1, v=2 нүктеде қиылысады.
Сонда 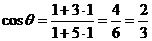


3- мысал. x=u cosv, y=sinv, z=av геликоидада жатқан u=0, u=a, v=0, v=1 қисықтармен шектелген төрт бұрыштың ауданын табыңдар.
Шешуі: Аудан  формуламен табылады. Мұндағы Д мына u =0, u=a, v=0, v=1 сызықтармен шектелген төрт бұрыш
формуламен табылады. Мұндағы Д мына u =0, u=a, v=0, v=1 сызықтармен шектелген төрт бұрыш
xu=+cosv, yu=sinv, zu=0, xv=-u sinv, yv=u cosv zv=a
E=  u
u  u=cos2V+sin2V+0=1 F=-usinv cosv+usinvcosv+0=0
u=cos2V+sin2V+0=1 F=-usinv cosv+usinvcosv+0=0
G=u2sin2v+u2cos2v+a2=u2+a2
Сонда 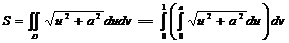 мына формуланы
мына формуланы
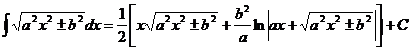 пайдалансақ
пайдалансақ
 Демек
Демек
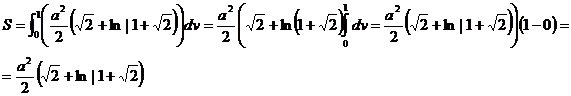
§ 61. Беттің екінші квадраттық формасы, беттегі қисық
Не нашли, что искали? Воспользуйтесь поиском: