
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тұрақты қисықтықты беттер
Әрбір нүктесінде толық қисықтың Кг – тұрақты болатын бет тұрақты толық қисықтықты бетғ, ал орта қисықтығы Ко- тұрақты болатын бет тұрақты орта қисықтықты бет делінеді. Қарапайым беттер үшін Kr- да, K0- да тұрақты және 0-ге тең боолады. Кезкелген цилиндрлық конустың беттерде толық қисықтығы тұрақты және Kr=0 болатын (себебі олар параболалық нүктелерден тұрады) беттер болады.
Толық қисықтығы тұрақты болатын айналу беттері де болады. Тік бұрышты Охуz координата жүйесінде П жазықтығы және онда жатқан L қиысығы берілсін. П жазықтығына Ou z координата жүйесін ендірейік. (Мұндағы Ou=Oxy  П) (379а-сурет-1) L жатық сызық болсын, оның Ou ғ нүктедегі теңдеуі z=f(u) болсын
П) (379а-сурет-1) L жатық сызық болсын, оның Ou ғ нүктедегі теңдеуі z=f(u) болсын  дейік.
дейік.
M нүкте L- де жатсын. L сызығы Оz осінен айналаса яғни  бұрыш (0,2п) аралықта өзгерсе L -дің әрбір M нүктесі центрі
бұрыш (0,2п) аралықта өзгерсе L -дің әрбір M нүктесі центрі  осінде жататын шеңберлер сызар еді. Онда айналу беттің паралельдері дейді. Охуz -дегі M(х,у,z) координатыболсын.
осінде жататын шеңберлер сызар еді. Онда айналу беттің паралельдері дейді. Охуz -дегі M(х,у,z) координатыболсын.




 z П L z
z П L z
 01
01
М Mo


 0 u
0 u


 0 y
0 y

х u
379-а сурет (1,2,3).
Онда x=ucos  , y=usin
, y=usin  , z=f(u) (*1)
, z=f(u) (*1)
Бұл L сызықтың Оz -тең айналуынан шыққан F беттің параметрлік теңдеуі болады. Оның жағындағы функциялар үздіксіз және
Ранг 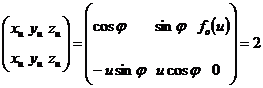
Сондықтан M  F0
F0 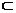 F болатын Fо - элементар бет болады. F жатық бет болады.
F болатын Fо - элементар бет болады. F жатық бет болады.  десек беттің векторлық теңдеуі
десек беттің векторлық теңдеуі
 =ucos
=ucos 
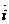 +usin
+usin 
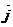 +f(u)
+f(u) 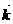 (*2) болады.
(*2) болады.
Мұндағы праметрлер u мен  . Координаттық сызықтар -
. Координаттық сызықтар -  тұрақты болса беттің меридианалар, u-тұрақтыболса паралельдері болады.
тұрақты болса беттің меридианалар, u-тұрақтыболса паралельдері болады.
(*2) ден  (u,
(u,  ),
),  u(cos
u(cos  , sin
, sin  , f1u(u);
, f1u(u);  (-u sin
(-u sin  , u cos
, u cos  , 0),
, 0), 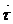 uv(0,0,f11uu(u)).
uv(0,0,f11uu(u)).
 u
u  (sin
(sin  , cos
, cos  , 0);
, 0); 

 (-ucos
(-ucos  , -usin
, -usin  , 0) Болатындықтан
, 0) Болатындықтан
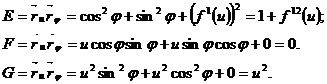
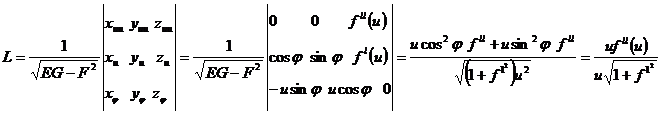
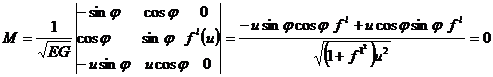
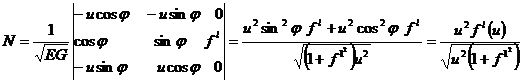
Бізде F=0, M=0 болды. Сондықтан координаттың тор қисықтық сызығынан жасалған. Сөйтіп айналу бетінде қисықтың сызықтары меридианы мен паралельдері болады екен. Сонда беттің M нүктедегі жатық қисықтығы
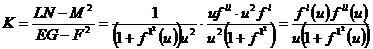 (61-22)
(61-22)
Нақты беттерді қарастырайық.
1) F сфера болсын. Оның радиусын r деген П жазықтықтағы теңдеуі z2+u2= 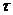 2 болар еді. Бұдан
2 болар еді. Бұдан 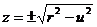 мұның плюсін алайық, сонда
мұның плюсін алайық, сонда 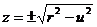 ,
, 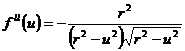 болады бұдан
болады бұдан  .
.
Сонда (61-22) бойынша  болып шығады. Демек сфераның кезкелген нүктесінде беттің толық қисықтығы
болып шығады. Демек сфераның кезкелген нүктесінде беттің толық қисықтығы 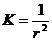 болады екен. сондықтан ол тұрақты болады және ол сан болады. Демек сфера тұрақты оң толық қисықтықты бет болады.
болады екен. сондықтан ол тұрақты болады және ол сан болады. Демек сфера тұрақты оң толық қисықтықты бет болады.
2) F -псевдосфера болсын. Псевдосфера деп трактрисаның (379-а сурет-2) өзінің осінен (Оғ -тең) айналуынан шыққан бетті айтады. (379-а сурет-3).
Практрисаның П жазықтықтағы параметрлік теңдеуі  (a -тұрақты). Бұдан
(a -тұрақты). Бұдан 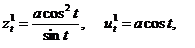

Мұның толық қисықтығы 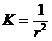 , тұрақты, теріс болады. Сонымен псевдосфера теріс толық қисықтықты бет болады екен. Орташа қисықтығы барлық нүктесіде тұрақты болатын бетті минималды бет дейді. Тек Геликоид сондай бет болады. Бірдей тұйық сызықпен шектелген беттердің ішінде ауданы ең аз болатын бет минималды бет болады.
, тұрақты, теріс болады. Сонымен псевдосфера теріс толық қисықтықты бет болады екен. Орташа қисықтығы барлық нүктесіде тұрақты болатын бетті минималды бет дейді. Тек Геликоид сондай бет болады. Бірдей тұйық сызықпен шектелген беттердің ішінде ауданы ең аз болатын бет минималды бет болады.
Не нашли, что искали? Воспользуйтесь поиском: