Изометрикалы беттер

Геометрияда қарастырылатын бейнелерге әдетте қатты денелік сипат беріледі, яғни геометриялық фигураларды кеңістікте қозғағанда олардың өлшемдіктері, ұзындығы ауданы, көлемі т.б. қасиеттері өзгермейді деп саналады. Бетті де осы көзқарасты түсініп, оны қатты бір дененің қабығы ретінде қарастырып келдік. Бетке бұдан өзге көзқараста қарауға да болады. Мысалы оны жиырылмайтын, сығылмайтын, иілгіш жұқа пленка (қабыршақ) ретінде қарастыруға болады. Сонда мұндай жұқа қабыршақты (бетті) июге, майыстыруға болады. Ол бет жиырылмайтын, сығылмайтын болғандықтан, ол бетте жатқан қисықтың доғасының ұзындығы т.б. беттің кейбір қасиеттері беттің ию, майыстыру процесінде өзгермейді.

Ені Ф және Ф¹ бет нүктелері арасында, ал беттерде жатқан сәйкес қисық доғалары ұзындықтары теңдей болатындай етіп 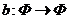биективтік сәйкестік орнатуға болатын болса, онда ол беттерді изометрикалы немесе беттесетін беттер деп атайды. f- ты изометрия дейді. Егер екі бет изометрикалы болса, онда оның бірі екіншісінен ию арқылы алынған делінеді. Сөйтіп беттің ию, майыстыру арқылы өзара тең емес, бірақ өзара изометрикалы әртүрлі беттер шығаруға болады.

S

A D

a) б)

в) г) B д) C

е) f) g)

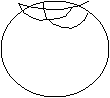
380-сурет

380-суретте жазықтықты (а-сурет) ию арқылы екі жақты бұрышқа (б-сурет), цилиндрлік бетке (в-сурет) айналдырған үш жақты бұрышта (г-сурет) жазу арқылы бұрышқа (д-сурет) айналдырған жазық бұрыштардың қосындысы 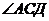- ға тең. Конусты бір жасаушысы боынша қисық бағытта қиып секторға айналдыруға болады.

f сфераны кесіп, кесілген бөлікті төмен қарата салған. Сонда f –тің д-ға айнлған. Бұлар әртүрлі, өзара тең емес фигуралар, бірақ бірі екіншісінен ию, майыстыру (жиырмай, сызбай) арқылы шыққан. Ф мен Ф ¹ С^к - классты жатық беттер, ал f: Ф → Ф ¹ - изометрия болсын Ф бетке (u, v) қисық сызықтық координаталар, Ф ¹-ке 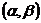қисық сызықтың координаталар ендірілген болса онда f бейнелеуді 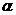= 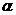(u, v), 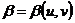теңдеумен беруге болар еді. Ф ¹ бетте u 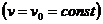координаты сызығын қарастырсақ

f бейнелеуде бұл сызық Ф ¹ беттің теңдеуі 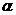= 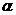(u, v₀), 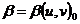болатын L сызығына көшер еді. L сызығын Ф ¹ беттегі u -сызығы деп атаймыз. Сөйтіп Ф -дағы u,v сызықтар үйірі Ф ¹ тегі u,v сызықтар үйіріне көшеді де Ф бетте екі параметрлеу 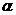, β параметрлерін және f бейнелеу нәтижесінде пайда болған u,v қиысу сызықтың параметрлеу. Ф мен Ф ¹ бтерді |u,v| параметрлеуді f бейнелеуге қарағанда ортақ дейміз. Сонда Ф беттің M нүктесінен координаталары (u, v) болғанда бұл нүктенің бейнесі M= f (M)-нің беттегі координаталрында f ке қарағанда ортақ параметризациялауда (u, v) болады.

Теорема. Екі Ф және Ф ¹ жатық беттер қисық сызықты координаттары бірдей нүктелердегі бірінші квадраттық формалдардың сәйкес коэфициенттері теңдей болатындай етіп параметризациялауға болатын жағдайды ғана, тек сол жағдайда ғана изаметрикалы болады.

Дәлелі. F:ф→ф¹ изометрика болсын. Ф бет [u, v] қисық сызықты координаталар арқылы параметрленген болсын. Онда f бейнелеу Ф бетте f -ке қарағанда ортақ (u, v) параметризация тудырады.

Ф тен l жатық сызық u=u(t), v=v(t) t I теңдеумен берілсін онда Ф¹ беттегі f(l)=L сызық теңдеуіде осындай болады.

Ал, f -изометриия болғандықтан f-түрлендіру кезкелген жатық сызық ұзындығы өзгертпейді.

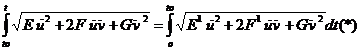
Ал, бұл кез келген t₀ үшін дұрыс болғаныдықтан

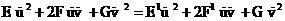
Ал, l сызық еркін алынғандықтан бұл теңдік кезкелген бағыт үшін, яғни кезкелген u, v үшін дұрыс болуы керек.

Сондықтан E=E¹, F=F¹, G=G¹ яғни беттің сәйкес нүктелеріндегі 1-квадраттың форма коэфициенттері теңдей болады.

Енді керісінше Ф және Ф¹ жатық беттерді Ф -тен u, v қисық сызықты координатты кезкелген M(u,v) нүктесі мен Ф¹ -тің осынадай u,v координаты M¹(u,v) нүктесі үшін беттің бұл нүктелеріндегі бірінші кваадратық формасының сәйкес коэфициенттері E(u,v)= E¹(u,v), F(u,v)= F¹(u,v), G(u,v)=G¹ (u,v) тең болатын дай етіп параметрлеуге болатын болсын.

M(u,v) →M¹(u,v) заңмен іске асатын F:ф→ф¹ биективтік бейкемуді қарастырайық. Онда кезкелген l ф жатық сызық және оның бейнесі f(M)=M¹ ф¹ үшін (*) формуланың орындалатыны түсінікті. Олай болса f бейнелеудегі беттегі сызық ұзындығы сақталады. Демек f изометрия болады.

Салдар. Егер Ф және Ф¹ бетер изометрикалы болса онда F:ф→ф¹ бейнелеудегі сәйкес нүктелер бір типке жатады. Яғни екеуі де не элипстік, не гиперболалық не параболалық нүктелер болады.

Өйткені Ф пен Ф¹ беттердің f бейнелеудегі сәйкес нүктелер үшін E=E¹, F=F¹, G=G¹ орындалатындықтан беттің беттің толық қисықтығы k екі нүктеде де бірдей болады. (Гаусс теоремасы бойынша) сондықтан салдар қортындысы дұрыс.

Бұл салдарды кезкелген екі жатық бет өзара изометрикалы бола бермейтіні шығады. Мысалы Элипстік цилиндр мен (ол параболалық нүктелерден тұрады) бірқуысты гиперболоид (бұл тек гиперболалық нүктелерден тұрады) Изоморфты болмайды.

Сонымен екі бет изометрикалы болса, онда оның бірі екіншісінен ию арқылы алынаған, бірі екіншісіне беттеседі делінеді.

Басқа бір бетке беттестіруге болатын бетті иілімді бет дейді.

жатық беттер «кіші аймақты» Иілімді, ал «үлкен аймақта» иілімді болмауы мүмкін (мысалы сфера сондай).

Бір рет екіншісінен ию арқылы алынса онда олар изометрикалы болғаны.

Дәлелденген теорема бойынша изометрикалы беттердің сәйкес нүктелеріндегі беттің бірінші квадраттық формасының сәйкес коэфициенттері теңдей болады. Сондықтан бетте жатқан сәйкес қиықтар доғасының ұзындығы теңдей болады.

62.2. Беттің ішкі геометриясы.

Бетті игенде, майыстырғанда ол бет бойында жататын қисық доғасының ұзындығы өзгермейтін болды.

Беттің және бетте жптқан фигуралардың бетінде жатқан сызық ұзындығына ғана тәуелді болатын қасиеттерін қарастырайық геометрия бөлігін беттің ішкі геометриясы дейді.

Ал, жатық беттер және онда жатқан фигуралар үшін беттің ішкі геометриясы деп олардың тек бірінші квадраттық формасымен анықталатын қасиеттерін зерттейтін геометрия бөлімін айтады.

Мысалы төмендегі ұғымдар беттің ішкі геометриясынан объектілері болады.

1. Бетттегі қисық доғасының ұзындығы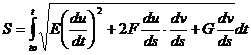

2. Беттегі қисықтар арасындағы бұрыш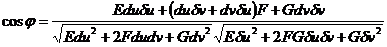

3. Бетте жатқан облыс ауданы 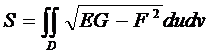Өйткені олар беттің бірінші Д квадраттық формасы арқылы анықталады.

Енді беттің ішкі геометрикасына кіретін басқа ұғымдармен мысалдарды қарастырайық.

Не нашли, что искали? Воспользуйтесь поиском: