Петерсон Кодацци және Гаусс формулалары

C^k классты Ғ жатық бет = (u,v) теңдеумен берілсін. Бұл функция үздіксіз функция болғандықтан ( _uu)_u=( _uv)_u, ( _uv)_v=( _vv)_u, ( _u)_v=( _v)_u (1*) блады.

Егер бұл дифференциалдауларды (яғни (62) фомуланы дифференциалдан) орындап. Ондағы _uu, _uv, _v, _u, _v мәндерін (62) бойынша орнына қойсақ сөйтіп оларды _u, _v, бойынша топтасақ мынадай үш векторлық теңдік аламыз.

Мұндағы _u, _v, сызықтық тәуелсіз болғандықтан, мұның коэффициенттері 0-гетең болады:

Сөйтіп осындай скаляр теңдік шы ғады. Бірақ олардың тек үшеуі ғана әртүрлі болады, қалғандары соларға тең.

Мысалы (62-1) – ден V арқылы (62-2) ден U арқылы туынды алып, одан шыққан өрнектегі орнына бұлардың (62)-дегі мәндерін қойып _u, _v, бойынша топтасақ:

Бұл екі теңдіктің сол жақтары тең болғандықтан оң жақтары да тең болады, және _u, _v, коэффициенттері өзара тең болады. Мысалы _u коэффициенттерін теңестірсек

3(*)

Мұндағы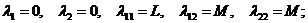

бұдан

Осы формуламен беттің толық қсықтығы деривациялық формулалар арқылы өрнектеледі.

Мұны (2*) дағы А₁=А₂ теңестіру арқылы таптық. Басқа коэффициентерді теңестіру (ұзақ есептеу арқылы) мына үш формуланы шығарып алуға болады

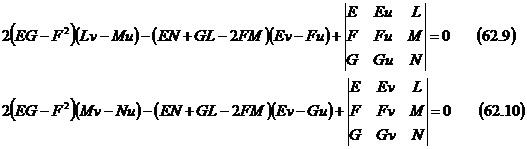
Мұның алғашқы екеуін П петерсон кодацци. Соңғысын Гаус формуласы дейді.

Бұл формулалар беттің 1-2 ква драттық формуласына коэффициентерін байланыстырады.

Не нашли, что искали? Воспользуйтесь поиском: