
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ОЦЕНКА ДОСТОВЕРНОСТИ РАЗНОСТИ МЕЖДУ ДВУМЯ ВЫБОРОЧНЫМИ СРЕДНИМИ
При оценке достоверности разности между результатами исследований при малом числе наблюдений определяется нормируемое отклонение или критерий Стьюдента-Фишера (tP)по формуле:
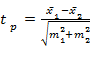 (1.5)
(1.5)
где 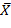 1и
1и 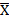 2 – средние арифметические значения полученных данных; m1и m2 – средние ошибки измерений.
2 – средние арифметические значения полученных данных; m1и m2 – средние ошибки измерений.
Значения tpпри разных уровнях достоверности (95 и 99 %) приведены в таблице 1.Таблица 1
| Число степеней свободы | Уровень достоверности | Число степеней свободы | Уровень достоверности | Число степеней свободы | Уровень достоверности | |||
| 95 % | 99 % | 95 % | 99 % | 95 % | 99 % | |||
| 12,71 | 63,66 | 2,18 | 3,06 | 2,07 | 2,81 | |||
| 4,30 | 9,92 | 2,16 | 3,01 | 2,06 | 2,80 | |||
| 3,18 | 5,84 | 2,14 | 2,98 | 2,06 | 2,79 | |||
| 2,78 | 4,60 | 2,13 | 2,95 | 2,06 | 2,78 | |||
| 2,57 | 4,03 | 2,12 | 2,92 | 2,05 | 2,77 | |||
| 2,45 | 3,71 | 2,11 | 2,90 | 2,05 | 2,76 | |||
| 2,36 | 3,50 | 2,10 | 2,88 | 2,04 | 2,75 | |||
| 2,31 | 3,36 | 2,09 | 2,86 | 2,04 | 2,70 | |||
| 2,26 | 3,25 | 2,09 | 2,84 | 2,02 | 2,70 | |||
| 2,23 | 3,17 | 2,08 | 2,83 | 2,02 | 2,66 | |||
| 2,20 | 3,11 | 2,07 | 2,82 | 1,98 | 2,62 |
В таблице 1 в графе «Уровень достоверности» помещены значения критерия Стьюдента-Фишера tp, показывающие, во сколько раз разность показателей должна при данном «Числе степеней свободы», или малом числе наблюдений, превышать свою среднюю ошибку для того, чтобы эта разность могла быть признана достаточно достоверной. При статистической оценке числа в графе «Число степеней свободы» равны числу произведенных наблюдений, уменьшенному на единицу, т.е.n – 1. Но если оценивается достоверность разности двух выборочных средних показателей, то число степеней n1 будет равно сумме числа произведенных наблюдений по двум выборочным средним, уменьшенной на две единицы, т. е. n1 = n1 + n2 – 2.
Если разность показателей больше суммы своих средних ошибок в 2,5 – 3,0 или хотя бы в 2,0 раза, то с вероятностью, определяемой по таблице 1, можно утверждать, что различие в величине показателей не случайно, а зависит от какой-то причины.
Пример. При хранении моркови двумя способами получены следующие данные (таблица 2).
Таблица 2
| Способы хранения | Выход стандартной части продукции по повторностям опытов, % | Среднее
арифметическое
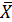
| |||||||
| Первый | 90,4 | 92,6 | 91,2 | 98,1 | 93,6 | 89,3 | 96,9 | 95,1 | 93,4 |
| Второй | 91,8 | 88,8 | 92,9 | 89,6 | 94,0 | 87,8 | 88,9 | 90,9 | 90,5 |
Требуется определить, случайна ли разность среднего выхода стандартной части корнеплодов моркови по первому и второму способам хранения, т.е. X1 – Х2 = 93,4 – 90,5=2,9%.Расчет производим по формуле 1.5. Для вычисления m1иm2 надо определить среднее квадратическое отклонение обеих сравниваемых величин по формуле 1.2. Отклонением dназывается разность значений повторностей каждого ряда опытов от средней арифметической этого ряда. Расчеты суммы квадратов отклонений по первому способу хранения моркови d1и второму способу d2приведены в таблице 3.Таблица 3
| dl | d2 | d12 | d22 |
| -3,0 | -1,3 | 9,00 | 1,69 |
| -0,8 | -1,7 | 0,64 | 1,87 |
| -2,2 | 2,4 | 4,84 | 5,76 |
| 4,7 | 0,9 | 22,09 | 0,81 |
| 0,2 | 3,5 | 0,04 | 12,25 |
| 4,1 | -2,7 | 16,81 | 7,29 |
| 3,5 | -1,6 | 12,25 | 2,56 |
| 1,7 | -0,5 | 2,89 | 0,25 |
| Σ68,56 | Σ68,05 |
Среднее квадратическое отклонение составляет:
по первому способу хранения моркови
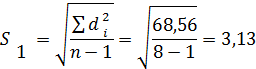
по второму способу
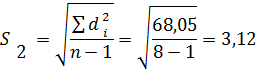
Средние ошибки определяют по формуле 1.4 (без учета нормированного отклонения t)
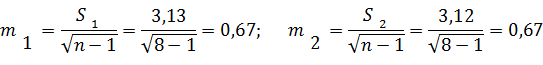
Затем находят значение tp

Величина tpнайдена равной 2,50 при n1 = 8 + 8 – 2=14. Оценивая значение tpпо таблице 1, в графе «Уровень достоверности 95 %» находим, что при n1=14 tPсоставляет 2,14, а фактически найден равным 2,50. Можно сделать вывод, что с вероятностью ошибки, меньшей 5%, выявлена неслучайная разница средних величин 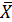 1и
1и  2 и, следовательно, достоверно установлена лучшая сохраняемость моркови по первому способу хранения.
2 и, следовательно, достоверно установлена лучшая сохраняемость моркови по первому способу хранения.
Не нашли, что искали? Воспользуйтесь поиском: