Методика изучения чисел 1-10 в специальной (коррекционной) школе VIII вида. Составьте фрагмент урока по теме «Ознакомление с числом 5».

Числа первого десятка и действия с ними изучаются в течение первого года обучения. Учащиеся знакомятся с каждым числом первого десятка в отдельности. Изучается образование каждого числа, обозначение его цифрой, счет в пределах этого числа, соотношение предметной совокупности, числа и цифры, определяя место числа в натуральном ряду чисел.

Наглядные пособия, используемые при изучении чисел первого десятка в 1-м классе

1. Предметные пособия:

а) предметы окружающей действительности: классная мебель, учебные принадлежности, природные материалы, фрукты, овощи, пуговицы, крючки, наперстки, игрушки (пуговицы и другие мелкие предметы объединяются в цепочки, нашиваются на картон);

б) специально изготовленные предметы для счета: палочки, арифметический ящик, счеты классные и индивидуальные, счетные подставки с вертикальными проволочками, рама с подвешенными на шнурках шариками (таких шнурков с шариками 10);

в) геометрические фигуры;

г) трафареты фруктов, овощей, грибов, зверей, птиц и т. д.

2. Иллюстративные пособия:

а) набор предметных картинок с изображением овощей, фруктов, зверей, самолетов, машин;

б) изображения предметов от 1 до 10;

в) картины с изображением как однородных, так и разнородных предметов, объединенных каким-нибудь сюжетом;

г) таблица «Числовая лесенка»;

д) набор подвижных цифр и знаков, фланелевые и наждачные цифры; резиновые штампы цифр; таблицы правильного начертания цифр; монетные кассы с набором монет в 1, 5, 10 к., 1, 5, 10 р.; серия таблиц по теме «Нумерация чисел первого десятка».

Учитель школы VIII вида должен постоянно помнить, что только демонстрация наглядных пособий не может обеспечить сознательного усвоения математических знаний. Необходимо использование материала в предметно-практической деятельности.

Изучение каждого числа первого десятка происходит в следующей последовательности.

На первом уроке дается понятие о числе и цифре. Цель этого урока — познакомить учащихся с образованием числа (путем присчитывания одной единицы к предшествующему числу), названием его, обозначением цифрой, научить писать цифру, показать место числа в числовом ряду, познакомить с соотношением количества элементов предметной совокупности, числа и цифры, рассмотреть количественные и порядковые отношения уже известного учащимся отрезка натурального ряда.

На втором уроке учащиеся закрепляют место данного числа в числовом ряду, получают понятие о втором способе образования предшествующего числа (путем отсчитывания одной единицы от данного числа), отрабатывают счет в прямом и обратном порядке. Учащиеся упражняются в сравнении количества элементов предметных совокупностей, чисел, установлении отношений равенства и неравенства между предметными совокупностями и числами (больше, меньше, равно).

На последующих уроках учащиеся знакомятся с составом этого числа из двух групп и действиями сложения и вычитания в пределах данного числа. Количество таких уроков зависит от величины изучаемого числа и состава класса.

К концу 1-го класса учащиеся должны понимать, что каждое число первого десятка образуется из предшествующего путем прибавления одной единицы, а если из числа вычесть единицу, то получится предшествующее число.

После знакомства с получением числа учитель учит обозначать это число цифрой, как печатной, так и рукописной. Цифра внимательно рассматривается, выделяются ее элементы, подыскиваются предметы, с которыми можно сравнить цифру. Это нужно для того, чтобы учащиеся лучше запомнили образ цифры, не смешивали его с другими цифрами. Далее надо обучить ребят письму цифр.

Последовательность знакомства с написанием цифр:

1. показ рукописного образца цифры, показ и письмо элементов цифры;

2. показ учителем письма цифры на доске (при этом обращается внимание на направление движения мела);

3. обводка (пальцем, указкой) модели цифры;

4. письмо цифры в воздухе;

5. письмо цифры на доске несколькими учениками;

6. письмо цифр в тетрадях по образцу.

При изучении каждого из чисел учащиеся учатся не только пересчитывать предметы и отвечать на вопрос «Сколько?», но и определять порядковый номер того или иного предмета (в зависимости от порядка, в котором проводится счет). Определение порядкового номера пересчитываемых предметов имеет большое значение для развития пространственных представлений, так как ученики знакомятся с порядковым отношением, местом предмета в ряду других: перед, между, за, около — это слова, которые указывают на пространственное положение предмета.

«Ознакомление с числом 5».

Цель: Ознакомление с числом и цифрой 5.

Задачи:

Образ.

познакомить с числом 5;

познакомить с получением числа 5;

изучить состав числа 5.

Воспит.

способствовать воспитанию, трудолюбия, любви к предмету.

Развив.

развивать речь, внимание, память, мышление учащихся;

формировать устойчивое внимание;

совершенствовать вычислительные навыки.

Ход урока

Организационный момент

Актуализация знаний учащихся.

Устный счет

Выходят к доске 4 человека. Берут карточки с цифрами. Располагают числа в порядке возрастания: 4 3 2 1.
– Назовите самое большое и самое маленькое число.
– Какое число находится между числами 2 и 4?
– Какое число следует за числом 1?

– Назови число предшествующее числу 4.

Весёлые задачки.

На пасеке 3 медвежонка,
Играли в прятки у бочонка.
Один в бочонок еле влез,
А сколько убежало в лес?
Ответ 2.

Изучение новой темы

Пред тобой – пятёрка братьев,
Дома все они без платьев,
А на улице, зато
Нужно каждому пальто. (5 пальцев)

- Сколько пальцев на руке? Ребята, кто мне поможет сосчитать?

На моей руке 5 пальцев,
5 хватальцев, 5 держальцев
Чтобы брать и отдавать,
а ещё чтоб сосчитать – 12345.

- У каждого пальца на руке есть своё имя как у человека. Ребята, а кто знает, как называются пальцы на руке? Назовите их. - Большой, указательный, средний, безымянный, мизинец.

- Рассмотрите звёздочки. Выберите ту звёздочку, у которой, столько лучей, сколько пальцев у вас на руке. Какую вы взяли звёздочку? Почему?

- Звёздочку с пятью лучами.

Физминутка

Обозначение числа цифрой

-Посмотрите на доску. Сколько в верхнем ряду красных кружков? (на доске 4 кружка)

- Положите в нижнем ряду столько же синих.

- Добавьте ещё один синий. Сколько стало?

- Число 5 будем обозначать цифрой 5.

- Каких кружков стало больше? Сравни: 4 <5, 5>4.

- Поставим число 5 в ряд натуральных чисел. За каким числом оно будет следовать?

Число 5 стоит в ряде натуральных чисел за числом 4. Один, два, три, четыре, пять. Мы каждый раз прибавляем одну отдельную единицу и получаем число на одну отдельную единицу больше предыдущего числа. Так и к числу 4 мы прибавили одну отдельную единицу и получили число 5, стоящее и следующее за числом 4.

- Сейчас мы будем учиться написанию цифры 5 в тетради.

- Цифра 5 состоит из 3 элементов: это прямая вертикальная линия, полукруг и прямая горизонтальная линия.

- Начинаем писать. Ставим ручку на 1/3 влево от верхнего правого угла клеточки, опускаемся через центр клеточки чуть ниже его, возвращаемся до центра и плавно уходим вправо вверх, закругляем, опускаемся по наклонной вниз и в 1/3 части нижней стороны клетки выписываем «клюшку». Ставим ручку в начальную позицию и уходим по стороне клетки на 1/3 вправо до угла». (Цифра 5 пишется в два приема с отрывом ручки.)

- Пропишите 1 строчку цифры5 в тетради.

- Теперь вы уже знаете не только число 5, но и какой цифрой на письме это число обозначается и из скольких элементов состоит.

Пальчиковая гимнастика

1,2,3,4,5 вышли пальчики гулять.

Погуляли, погуляли, и домой пошли опять.

(Ладони смотрят друг на друга, пальцы соединяем и разъединяем попарно)

6. Закрепление нового материала.

«Игра найди своё место» Ребята, нужно выйти к доске, взять и расположить карточки по порядку от 1 до 5.

- А теперь хором проговорим в последовательности в прямом и обратном порядке.

- На каком месте в натуральном ряде чисел стоит число 5?

7. Итог урока

Методика решения простой арифметической задачи в специальной (коррекционной) общеобразовательной школе VIII вида. Составьте фрагмент конспекта урока по анализу задачи. Задача: «На первой полке 5 книг, а на второй полке на 2 книги больше. Сколько книг на второй полке?».

МЕТОДИКА РЕШЕНИЯ ПРОСТЫХ АРИФМЕТИЧЕСКИХ ЗАДАЧ

Простой арифметической задачей называется задача, которая решается одним арифметическим действием. Простые задачи играют чрезвычайно важную роль при обучении учащихся математике. Именно простые задачи позволяют раскрыть основной смысл и конкретизировать арифметические действия, сознательно овладеть теми или иными математическими знаниями. На простой задаче учитель впервые знакомит учащихся со структурой задачи, показывает, что значит решить задачу, вооружает их основными приемами решения задач.

В школе VIII вида решаются задачи, раскрывающие конкретный смысл арифметических действий (I группа). Это задачи на нахождение суммы и на нахождение остатка (1-й класс), на нахождение произведения (суммы одинаковых слагаемых), на деление на равные части (3-й класс), на деление по содержанию (3-й класс).

Решаются также задачи, раскрывающие новый смысл арифметических действий. Это задачи, связанные с понятием разности и отношения (II группа):

1. Увеличение и уменьшение числа на несколько единиц.

2. Разностное сравнение чисел с вопросами «на сколько больше...», «на сколько меньше...».

3. Увеличение и уменьшение числа в несколько раз.

4. Краткое сравнение чисел или нахождение отношения чисел с вопросами: «Во сколько раз больше...», «Во сколько меньше...».

К задачам, раскрывающим зависимость между компонентами результатами арифметических действий (III группа), относятся задачи на нахождение неизвестного слагаемого, на нахождение не известного уменьшаемого, неизвестного вычитаемого.

В школе VIII вида на каждом году обучения учащиеся знакомятся с новыми видами простых задач. Постепенное введение их объясняется различной степенью трудности математических понятий, местом изучения тех арифметических действий, конкретный смысл которых они раскрывают.

Сюжетные задачи составляются с однородными и неоднородными предметами, в них входят обобщающие слова. При обучении решению задач определенного вида целесообразнее сначала предъявлять сюжетные задачи с однородными предметами. Затем вводятся сюжетные задачи с однородными предметами, отличающимися теми или иными признаками: цветом, размером, материалом и т. д. Наконец, вводятся задачи, в которых имеются обобщающие слова. Вопрос записывается не полностью, а с помощью символов: круглая, квадратная или фигурная скобка символизирует сумму, а знак вопроса (?), что эта сумма неизвестна.

Знакомство с простой задачей

Чтобы решить задачу, ученики должны уметь решать арифметические примеры, слушать, а затем (со 2-го класса) читать задачу, повторять задачу по вопросам, по краткой записи, по памяти, выделять в задаче составные компоненты (условие, числовые данные, вопрос), «опредмечивать» содержание задачи или давать краткую форму ее записи, решать задачу (выбирать правильно действие и производить вычисление), записывать решение, формулировать ответ устно и записывать его, проверять правильность решения задачи.

В 1-м классе учащиеся учатся решать задачи на нахождение суммы и остатка. Эти задачи вводятся впервые при изучении чисел первого десятка. Предъявляя задачу, учитель должен сразу познакомить учащихся с термином «задача». На этом же этапе учитель знакомит учащихся со структурой задачи (условием, числовыми данными, вопросом).

Решение задач на увеличение (уменьшение) числа на несколько единиц и других, при решении которых раскрывается новый смысл арифметических действий, опирается на понимание учащимися смысла выражений: «на столько-то единиц больше (меньше)», «во столько-то раз больше (меньше)» и т. п. Поэтому перед введением таких задач необходимо раскрыть смысл этих выражений.

Этапы:

1) работа над содержанием задачи; установл зависимости между данными и искомым.разбор непонятных слов, чтение текста, запись условия, воспроизведение текста.

2) поиск решения задачи; отвечая на вопросы учителя, поставленные в определенной логич последовательности, подводятся к составлению плана решения задач и выбору действий. Намечаются план и последовательность действий. Разбор задачи можно начинать от главного вопроса задачи (снизу)

3) решение задачи; учащиеся осуществляли поиск решения задачи, они готовы устно сформулировать вопросы задачи и назвать действия.

Учитель спрашивает: «Во сколько действий задача? Какой первый вопрос? Каким действием можно ответить на этот вопрос?» И т. д.После этого учащимся предлагается записать решение.

4) формулировка ответа;

5) проверка решения задачи, функция контроля ослаблена.

В младших классах необходимо:

-Проверять словесно сформулированные задачи, производит действия над предметами, если, конечно, это возможно. Например: «У ученика было 15 р. Он купил 5 тетрадей по 2 р. Сколько денег у него осталось?» После решения задачи ученик берет по 2 р. 5 раз и считает, сколько всего денег. Потом из 15р. вычитает 10 р., получается 5 р.

-Проверять реальность ответа (соответствие его жизненной действительности).

-Проверять соответствие ответа условию и вопросу задачи.

6) последующая работа над решенной задачей.1. Ставятся узловые вопросы по содержанию задачи. Например:

Сколько дней дети собирали яблоки с пришкольного участка?

Известно ли, сколько яблок дети собрали в первый день (во второй день, в третий день)?

Что неизвестно в задаче?

Что нужно узнать в задаче?

Можно ли сразу ответить на главный вопрос задачи?

Какого данного для этого не хватает?

ТРУДНОСТИ:

1. Привнесение лишнего вопроса и действия.

2. Исключение нужного вопроса и действия.

3. Несоответствие вопросов действиям: правильно поставленные вопросы и неправильный выбор действий или, наоборот, правильный выбор действий и неверная формулировка вопросов.

4. Случайный подбор чисел и действий.

5. Ошибки в наименовании величин при выполнении действий: а) наименования не пишутся; б) наименования пишутся ошибочно, вне предметного понимания содержания задачи; в) наименования пишутся лишь при отдельных компонентах.

6. Ошибки в вычислениях.

7. Неверная формулировка ответа задачи

Следует избегать натаскивания в решении задач определенного вида, надо учить сознательному подходу к решению задач, учить ориентироваться в определенной жизненной ситуации, описанной в задаче, учить выделению данных и искомого задачи, установлению взаимосвязи между ними, осознанному выбору действий.

Тема. Задачи на увеличение (уменьшение) числа на несколько единиц (с одним множеством предметов).

Тип урока: комбинированный.

Цель: познакомить детей с решением задач на увеличение (уменьшение) числа на несколько единиц.

Задачи:

Образовательные: отрабатывать навыки сложение и вычитания в пределах 10.

Воспитательные: воспитывать аккуратность при работе в тетради.

Корекционно-развивающие: развивать логическое мышление, по средствам решения задач, развивать внимание и фонематическое восприятие, за счёт прослушивания текста задач.

Ход урока

Организационный момент

Устный счёт: посчитайте по порядку от 3-6, в обратном порядке от 7- 3, назовите соседей числа 5, назовите соседей числа 8, назовите число большее чем 2 на один, назовите число меньшее 6 на один.

Решение примеров: 3+5; 6-2; 7 +3; и т.д.

Задача: «На первой полке 5 книг, а на второй полке на 2 книги больше. Сколько книг на второй

1. Чтение задачи учителем 2 раза. 2. Вопросы по задаче: а) что означает число 5? что означает число 3? б) сколько книг на первой полке? сколько книг на второй полке? Ещё раз повторение задачи (что нам известно, что надо найти). 3 Решение задачи: 5+2=7 к. Если дети знают все буквы, они пишут слова Задача и Ответ. Если не знают, то решение задачи пишется как пример, но только по середине. При решении задачи можно пользоваться наглядно-дидакт материалами, которые раздаются детям и вешаются на доску.

44. Предложите приемы организации устного счета в начальных классах специальной (коррекционной) школы VIII вида. Устный счет является неотъемлемой частью почти каждого урока математики в школе VIII вида. Устный счет может проводиться не обязательно в начале урока, но в середине, конце, в зависимости от целей устного счета на уроке. Устный счет должен быть тесно связан с темой. Формы восприятия устного счета. 1) Беглый слуховой (читается учителем, учеником, записано на магнитофоне) – при восприятии задания на слух большая нагрузка приходится на память, поэтому учащиеся быстро утомляются. Однако такие упражнения очень полезны: они развивают слуховую память. 2) Зрительный (таблицы, плакаты, записи на доске, счеты, диапозитивы) – запись задания облегчает вычисления (не надо запоминать числа). Иногда без записи трудно и даже невозможно выполнить задание. Например, надо выполнить действие с величинами, выраженными в единицах двух наименований, заполнить таблицу или выполнить действия при сравнении выражений. 3) Комбинированный. А так же: - обратная связь (показ ответов с помощью карточек). - задания по вариантам (обеспечивают самостоятельность) - упражнения в форме игры (молчанка, продолжи цепочку, стук-стук, хлопки). Упражнения: 1. Обычные примеры. 2. Магические квадратыиспользуются для отработки навыков сложения и вычитания. Квадрат разделён на 9 частей. В центре записана сумма, которая должна получиться при сложении трёх чисел в каждой строке и каждом столбце. Задача: вставить пропущенные числа.

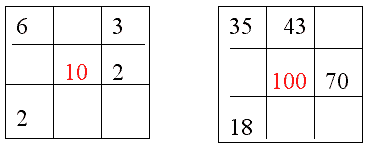
3. Круговые примеры.Смысл данного задания в том, что каждый последующий пример начинается с результата, полученного в предыдущем примере. Можно использовать при отработке различных вычислительных приёмов. 4. Полезно устно решать несложные задачи различных типов.

• Простые задачи на сложение и вычитание
• Простые задачи на умножение деление

5.выражения можно давайть в форме таблицы.

45. Раскройте методику формирования знаний конкретного смысла арифметического действия умножения. Впервые в 3-м классе учащиеся школы VIII вида знакомятся с новыми арифметическими действиями умножением и делением, составляют, заучивают таблицы умножения и деления чисел 2, 3, 4, 5 с ответами, не превышающими число 20. Лучшему осознанию смысла действия умножения способствует подготовительная рабо­та: счет равными группами предметов, а также счет по 2, 3, 4, 5 до 20. С этой целью учитель готовит наглядные пособия, раздаточ­ный материал. Такими пособиями служат учебные принадлежнос­ти, природный материал, игрушки, изображения предметов в виде трафаретов, разнообразные рисунки и т. д. Причем желательно объединять предметы, которые встречают­ся группами в жизненных условиях. Например, соединять варежки, перчатки, носки в пары, яйца - в десятки, пальцы рук - в группу по 5, колеса автомобиля - по 4, ножки табуретки - по 3 и т. д. 2 + 2 + 2 + 2 + 2 + 2 + 2 = Ребята, давайте решим этот пример. 2 + 2 + 2 + 2 + 2 + 2 + 2 = 14 Слагаемые у нас одинаковые? Сколько у нас их? Нам неудобно складывать такое большое количество слагаемых. Нам лучше сложение заменить умножением. Значок умножения «*». Число 2 взяли 7 раз, поэтому мы запишем 2 * 7 = 14

Не нашли, что искали? Воспользуйтесь поиском: