Однородные координаты (ОК) и

однородное координатное преобразование (ОКП)

Для преобразования может потребоваться цепочка операций, которую надо выполнить только операцией умножения и которая некоммутативна (АВ¹ВА), т.е. порядок умножения является важным.

Матрица преобразования 2х2 не выполняет операцию переноса (не путать сдвиг с переносом), но если выразить точки в ОК, то все основные преобразования будут реализованы за счёт операции умножения.

Все пакеты графических программ работают с ОК, которые применяются внутри самого пакета и недоступны для программиста.

Реализуются однородные координаты введением третьей компоненты в векторы положения точек P и P*, т.е. в виде || х у 1 || и || х* у* 1 ||. Матрица преобразования после этого становится матрицей размера 3х2: .

Введение третьей строки необходимо для выполнения умножения. Тогда,

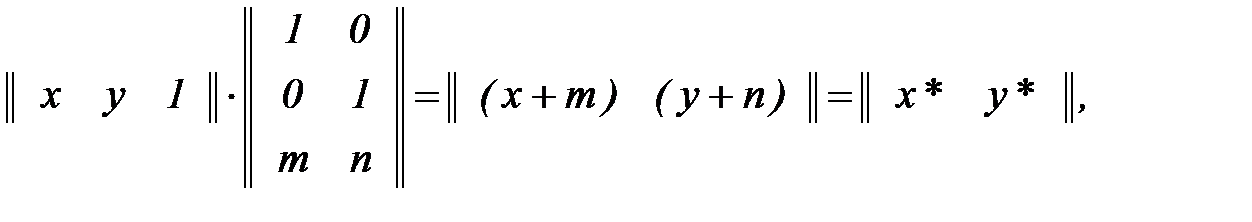
откуда следует, что константы m и n вызывают перенос х* и у* относительно х и у.

Так как матрица 3х2 не является квадратной, она не имеет обратной матрицы. Кроме того, исходная точка задана в ОК, а результат преобразования в обычных координатах. Устраним эти недостатки следующим приёмом: дополним матрицу преобразования 3Х2 до квадратной матрицы размером 3х3 следующим столбцом . Тогда

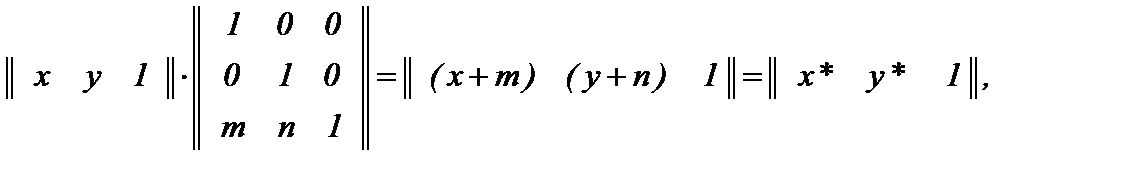
Так как третья дополнительная координата (обозначим её в общем случае h) равна 1, то выполнено преобразование в пространстве, ограниченном плоскостью h=1. Если h¹1, то преобразованные обычные координаты получаются нормализацией ОК, т.е. х*=Х/h и у*=У/h.

Если матрицу преобразования 3х2 дополнить третьим столбцом общего вида, то в результате ОКП получим

,

где h=рх+qy+1, т.е. это уравнение плоскости странстве (рх+qy-Н+1=0).

Таким образом:

Представление двухмерного вектора трехмерным или в общем случае n-мерного вектора (n+1) -мерным вектором называется однородным координатным преобразованием, которое выполняется в (n+1)- мерном пространстве, а конечные результаты в n -мерном пространстве получаются с помощью обратного преобразования, т.е. деления координат на величину h.

Матрица преобразования общего вида размера 3х3 для двухмерных однородных координат может быть условно подразделена на четыре части:

.

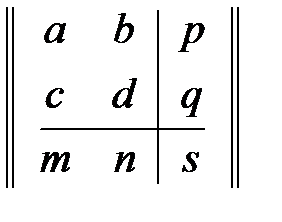a, b, c, d управляют изменением масштаба, сдвигом и вращением;

m и n управляют переносом;

p и q – управляют получением проекций;

элемент s – управляет полным изменением масштаба.

Не нашли, что искали? Воспользуйтесь поиском: