Примеры решения типовых задач. Задача 1. Прямая проходит через точки А(5,3) и В(6,8)

Задача 1. Прямая проходит через точки А(5,3) и В(6,8). К прямой применяется ОКП, заданное матрицей с последующим проецированием на плоскость Н=1. Составить уравнение результирующей прямой.

Решение.

Запишем матрицу Р, задающую прямую в ОК .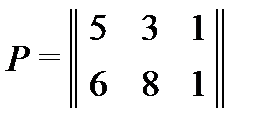

Найдём матрицу Р^*, получающуюся после применения ОКП .

Выполним операцию проецирования на плоскость Н=1. Для этого нормализуем полученные координаты ,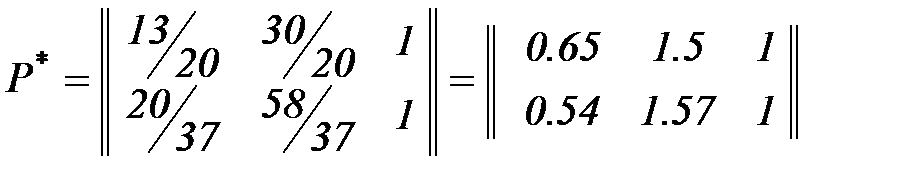

т.е. получена прямая, проходящая через точки А ^*(0.65, 1.5) и В *(0.54, 1.57).

Запишем уравнение прямой А*В*

,

а уравнение прямой АВ: .

т.е. мы трансформировали прямую 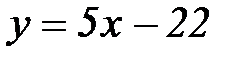в .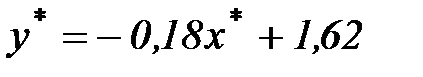

Задача 2. Найти матрицу ОКП, трансформирующую изображение, заданное матрицей Р в изображение, заданное матрицей Р ^*

^.

Решение: Р^* = Р Т, откуда Т = Р^-1 Р^*.

1. Найдем определитель матрицы Р, разложив её по элементам первой строки

Найдём алгебраические дополнения каждого элемента матрицы Р

Из алгебраических дополнений составим матрицу А и после её транспонирования получим матрицу А^t

^.

Получим обратную матрицу , после чего найдём матрицу ;

.

Выполним проверку правильности нахождения матрицы Т, т.е Р ´ Т = Р^*:

.

Задача 3. Составить матрицу ОКП, трансформирующего точку (x, y,z, 1) в точку ((x+5y+2z), (6x+y+4z), (2x+3y+z), 1)).

Решение. Запишем ,

что возможно, исходя из правил перемножения матриц, когда матрица

.

Не нашли, что искали? Воспользуйтесь поиском: