Базовые преобразования в ОК для плоскости

При записи сложного выражения (цепочки) удобно различать матрицы преобразований. Поэтому обозначим:

М(Т) – матрица преобразования переноса на вектор Т(t_x t_y);

M(R(a)) – матрица поворота относительно начала координат на угол a;

М(Е) – матрица преобразования масштаба на вектор Е(е_x е_y);

М(Сдв) – матрица линейного преобразования (сдвига)

М(От) – матрица отображения

Тогда для плоскости основные преобразования в ОК исходной точки Р(х, у) в точку Р*(х*, у*) запишутся следующим образом:

Преобразование масштаба на вектор Е(е_х е_у):

P* = P М(Е), где М(Е) .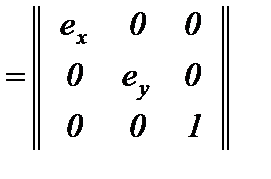

Преобразование переноса на вектор T(t_х t_у)

Р*=Р·М(Т), где М(Т) .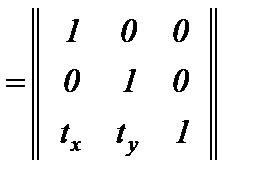

Преобразование поворота относительно начала координат на угол a:

Р*= Р М(R(a)), где М(R(a)) .

Преобразование отображения на вектор От(от_х от_у)

Р*=Р·М (От), где М(От) .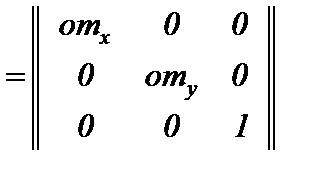

Преобразование сдвига на вектор Сд(сд_х сд_у)

Р*=Р·М (Сд), где М(Сд) .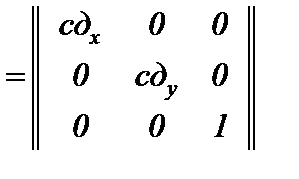

Не нашли, что искали? Воспользуйтесь поиском: