Теоретические сведения. Базовые понятия

Будем предполагать, что несколько переменных (объясняющих переменных, предикторов, факторных признаков, регрессоров) оказывают воздействие на значения зависимой переменной Y (отклик, результативный признак), т.е. имеет место зависимость.

В этом случае целесообразно строить уравнение множественной регрессии.

Множественная регрессия – уравнение связи зависимой переменной с независимыми переменными :

Линейное уравнение множественной регрессии имеет вид

(7.1)

где - параметры уравнения.

Пусть имеется п -наблюдений, тогда исходные данные представимы в виде матрицы размерности п на р и вектора размерности п:

(7.2)

Все элементы i -ой строки и i -ого элемента вектора Y_i - результаты i -ого наблюдения. Будем предполагать, что все наблюдения независимы и получены примерно в одинаковых условиях. В этом случае набор данных, определяемый соотношениями (7.2) называют пространственной выборкой или пространственными данными (cross section data). На практике эти значения часто получаются как результаты некоторого эксперимента, поэтому их часто называют наблюдаемыми или экспериментальными или эмпирическими значениями.

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Идея этого метода была подробно рассмотрена в лабораторной работе №5 «Линейная парная регрессия» (ЛР №5) [1]. Все соображения и выводы применимы и в случае множественной линейной регрессии с поправкой на количество факторов.

При использовании линейного уравнения множественной регрессии справедливо соотношение

,

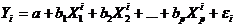где e_i, - случайные компоненты, которые также называют случайными членами или возмущениями или регрессионными остатками.

Присутствие в этом соотношении случайной компоненты e_i, обусловлено следующими причинами:

- ошибками спецификации, то есть отбора факторов, и выбора связи между явлениями;

- ошибками измерения.

Будем полагать, что относительно e выполняется ряд утверждений, известных как условия Гаусса-Маркова:

1. Равенство нулю математического ожидания регрессионных остатков:

;

2. Постоянство дисперсии регрессионных остатков (гомоскедастичность остатков):

;

1. Отсутствие систематической связи (корреляции) между значениями регрессионных остатков в любых двух наблюдениях: ;
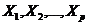2. - неслучайные величины.

Для определения параметров уравнения множественной линейной регрессии по МНК составляется сумма

.

Она равна сумме квадратов отклонений (остатков) наблюдаемых (эмпирических) значений отклика от теоретических значений 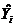в точке , при этом - теоретические значения отклика в i -ом наблюдении.. Величина суммы зависит от коэффициентов . Цель метода наименьших квадратов (МНК) заключается в выборе таких оценок , для которых сумма квадратов отклонений (остатков) будет минимальной.

Для того чтобы найти набор коэффициентов , которые доставляют минимум функции , используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных

В результате преобразований получаем следующую систему нормальных уравнений:

(7.3)

Для ее решения может быть применен любой известный метод решения системы линейных уравнений.

Коэффициенты в уравнении (7.3) называются коэффициентами множественной регрессии. Величина коэффициента показывает среднее изменение отклика Y при изменении фактора X_j на единицу.

Другой вид уравнения множественной регрессии - уравнение регрессии в стандартизованном масштабе:

(7.4)

где: - стандартизованные переменные;

, - число неизвестных;

, - средние значения;

- средние квадратические отклонения;

-стандартизованные коэффициенты регрессии.

В силу того, что стандартизованные переменные заданы как центрированные (средние значения ) и нормированные (средние квадратические отклонения ), стандартизованные коэффициенты регрессии сравнимы между собой, и с их помощью можно ранжировать факторы по силе их воздействия на результат.

Для определения коэффициентов уравнения множественной регрессии в стандартизованном масштабе так же применим МНК. Коэффициенты можно получить, решая систему, аналогичную системе (7.3). Эту систему можно преобразовать, и тогда, стандартизованные коэффициенты регрессии определяются из следующей системы уравнений:

, (7.5)

где

§ - коэффициент парной корреляции между факторами X_i и X_j,

§ - коэффициент парной корреляции между откликом Y ифактором X_j.

Отметим, что связь коэффициентов множественной регрессии со стандартизованными коэффициентами описывается соотношением

. (7.6)

Стандартизованный коэффициент регрессии показывает, на сколько величин в среднем изменится отклик при увеличении j-го фактора на одну величину .

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

(7.7).

Средний коэффициент эластичности показывает на сколько процентов в среднем изменится отклик при изменении его среднего значения фактора X_j на один процент, при неизменном значении остальных факторов.

Не нашли, что искали? Воспользуйтесь поиском: